Zestaw użytkownika nr 2708_6862
Feryjny zestaw maturanyoby nie feralny14 Lutego 2011
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 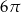 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 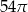 B)
B) 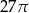 C)
C) 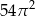 D)
D) 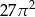
Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 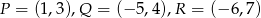 .
.
Suma drugiego, czwartego i szóstego wyrazu ciągu arytmetycznego jest równa 42, zaś suma kwadratów wyrazów drugiego i trzeciego jest równa 185. Wyznacz pierwszy wyraz i różnicę tego ciągu.
W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu opisanego ma długość 19 cm. Oblicz pole tego trójkąta.
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 2, a krawędź boczna długość 6.
Rozwiązaniem równania 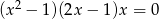 nie jest liczba
nie jest liczba
A) 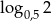 B)
B) 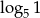 C)
C) 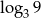 D)
D) 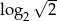
Okrąg o równaniu 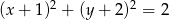 :
:
A) nie przecina osi 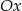 ,
,
B) nie przecina osi 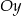 ,
,
C) przechodzi przez początek układu współrzędnych,
D) przechodzi przez punkt 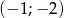 .
.
Wyrażenie 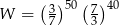 jest równe
jest równe
A) 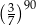 B)
B) 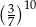 C)
C) 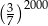 D) 1
D) 1
Dany jest ciąg arytmetyczny 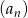 dla
dla 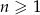 , w którym
, w którym 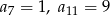 .
.
- Oblicz pierwszy wyraz
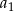 i różnicę
i różnicę  ciągu
ciągu 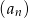 .
. - Sprawdź, czy ciąg
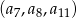 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 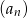 miała wartość najmniejszą.
miała wartość najmniejszą.
Wiedząc, że  jest kątem ostrym oraz
jest kątem ostrym oraz 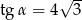 oblicz wartość wyrażenia
oblicz wartość wyrażenia 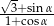 .
.
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia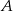 – na każdej kostce wypadła nieparzysta liczba oczek,
– na każdej kostce wypadła nieparzysta liczba oczek,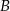 – suma wyrzuconych oczek jest nie mniejsza niż 8.
– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 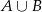 .
.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 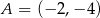 oraz
oraz 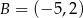 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 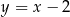 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
W pewnej szkole liczącej 500 uczniów 80% uczy się języka angielskiego, 49% – języka rosyjskiego, a 37% uczy się obu tych języków. Wynika stąd, że liczba uczniów, którzy nie uczą się żadnego z tych języków, to
A) 37 B) 167 C) 50 D) 40
Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma miarę 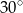 . Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
. Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu.

