Zestaw użytkownika nr 2737_6144

ANALIZA MATEMATYCZNAPRZYKŁADOWE ZADANIA

Zadanie 1

Dana jest funkcja

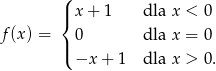
( |{ x + 1 dla x < 0 f(x ) = 0 dla x = 0 |( −x + 1 dla x > 0.

Wykaż, że funkcja ta nie jest ciągła w punkcie 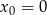x0 = 0 .

Zadanie 2

Wyznacz przedziały monotoniczności funkcji 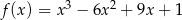3 2 f(x) = x − 6x + 9x + 1 .

Zadanie 3

Dana jest funkcja 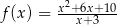x2+6x+10- f(x ) = x+ 3 .

Określ przedziały monotoniczności tej funkcji.
Znajdź ekstrema lokalne funkcji f.

Zadanie 4

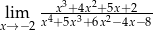Oblicz granicę --x3+-4x2+-5x+-2-- xli→m−2x4+ 5x3+ 6x2− 4x− 8 .

Zadanie 5

Oblicz granicę funkcji 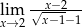-x−-2--- lxi→m2 √x−1− 1 .

Zadanie 6

Wykaż, że funkcja 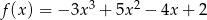3 2 f (x) = − 3x + 5x − 4x + 2 nie ma ekstremum. Czy funkcja 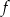jest malejąca?

Zadanie 7

Oblicz granicę funkcji 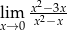x2−-3x lxi→m0 x2−x .

Zadanie 8

Wyznacz przedziały monotoniczności i ekstrema lokalne funkcji 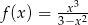-x3- f(x) = 3−x2 .

Zadanie 9

Dla jakich wartości parametru 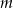funkcja

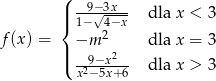
( --9−3x-- ||{ 1− √4−x- dla x < 3 f(x ) = −m 2 dla x = 3 || 9−x2 ( x2−-5x+-6 dla x > 3

jest ciągła w zbiorze liczb rzeczywistych?

Zadanie 10

Wyznacz ekstrema lokalne funkcji 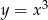3 y = x .

Zadanie 11

Oblicz z deﬁnicji pochodne jednostronne funkcji 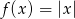f(x) = |x| w punkcie x0 = 0 .

Zadanie 12

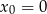Oblicz granicę funkcji 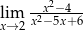-x2−4--- lxi→m2 x2− 5x+ 6 .

Zadanie 13

Wyznacz ekstrema lokalne funkcji 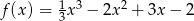1 3 2 f (x) = 3x − 2x + 3x− 2 .

Zadanie 14

Suma dwóch liczb równa jest 6. Znajdź te liczby, jeśli wiadomo, że suma podwojonego kwadratu jednej z nich i kwadratu drugiej jest najmniejsza z możliwych.

Zadanie 15

Wyznacz dwie liczby całkowite różniące się o 6, których iloczyn jest możliwie najmniejszy.

Zadanie 16

Liczbę 7 dzielimy na trzy części tak aby pierwsza była dwa razy większa od drugiej. Jak należy dokonać podziału, aby suma kwadratów wszystkich trzech części była najmniejsza?

Zadanie 17

Suma trzech liczb rzeczywistych dodatnich jest równa 13. Druga liczba jest trzy razy większa od pierwszej. Wyznacz trzy liczby spełniające podane warunki tak, aby suma ich kwadratów była najmniejsza.

Zadanie 18

Liczbę dodatnią przedstaw w postaci sumy dwóch takich składników, aby suma ich sześcianów była najmniejsza.

Zadanie 19

Suma kwadratów trzech kolejnych ujemnych liczb całkowitych parzystych jest równa 116. Wyznacz te liczby.
Wyznacz takie trzy kolejne liczby całkowite parzyste, których suma kwadratów jest najmniejsza z możliwych.

Zadanie 20

Wyznacz takie dwie liczby o sumie 100, których suma kwadratów jest najmniejsza.

Zadanie 21

Liczbę 49 rozłóż na dwa dodatnie składniki tak, aby ich iloczyn był największy. Podaj wartość iloczynu.

Zadanie 22

Liczbę dodatnią przedstaw w postaci sumy dwóch takich składników, aby suma ich kwadratów była najmniejsza.

Zadanie 23

Liczbę przedstaw w postaci różnicy dwóch liczb tak, aby suma kwadratów tych liczb była najmniejsza.

Zadanie 24

Znajdź liczby i 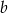wiedząc, że suma liczby i potrojonej liczby 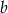jest równa 36, a iloczyn liczb a i b jest największy z możliwych.

Arkusz Wersja PDF