Zestaw użytkownika nr 2753_3779
Zestaw użytkownika
nr 2753_3779
W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie mają jednakową długość. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy.
Podstawą graniastosłupa prostego jest trójkąt prostokątny o przyprostokątnych mających długości 1 i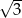 
. Podaj miary kątów między sąsiednimi ścianami bocznymi tego graniastosłupa.
Oblicz wysokość graniastosłupa sześciokątnego prawidłowego, wiedząc, że krawędź podstawy ma długość 5cm, zaś najdłuższa przekątna graniastosłupa jest 4 razy dłuższa od najkrótszej przekątnej podstawy.
W graniastosłupie prawidłowym trójkątnym o krawędzi podstawy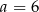 
przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze 
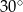. Oblicz
- długość przekątnej ściany bocznej,
- długość wysokości graniastosłupa,
- objętość i pole powierzchni całkowitej.
Krawędź boczna ostrosłupa prawidłowego czworokątnego jest nachylona do płaszczyzny podstawy pod kątem 
takim, że 
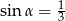. Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
Tangens kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa prawidłowego czworokątnego jest równy 
. Oblicz tangens nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.
Wysokość ostrosłupa prawidłowego sześciokątnego jest równa 6 cm i stanowi 
długości krawędzi podstawy.
- Oblicz miarę kąta nachylenia ściany bocznej do podstawy.
- Oblicz objętość ostrosłupa
Krawędź podstawy ostrosłupa trójkątnego prawidłowego jest równa 6. Jego objętość jest równa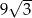 
. Wyznacz długość wysokości ściany bocznej ostrosłupa.
Wszystkie krawędzie ostrosłupa prawidłowego czworokątnego mają tę samą długość. Oblicz kąt nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Odległość środka podstawy ostrosłupa prawidłowego czworokątnego od krawędzi bocznej równa się 
, a kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się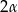 
. Oblicz wysokość ostrosłupa.
