Zestaw użytkownika nr 2845_7803
Zestaw użytkownika
nr 2845_7803
Rozwiązaniem równania 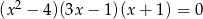 nie jest liczba
nie jest liczba
A) 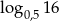 B)
B) 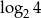 C)
C) 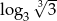 D)
D) 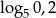
Wyrażenie 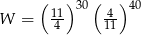 jest równe
jest równe
A) 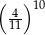 B)
B) 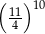 C)
C) 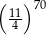 D) 1
D) 1
4,5% liczby  jest równe 48,6. Liczba
jest równe 48,6. Liczba  jest równa
jest równa
A) 108 B) 48,6 C) 1080 D) 4,86
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
![]()
A) 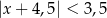 B)
B) 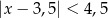 C)
C) 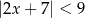 D)
D) 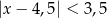
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 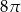 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 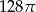 B)
B) 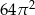 C)
C) 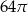 D)
D) 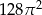
Wskaż 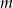 , dla którego funkcja liniowa
, dla którego funkcja liniowa 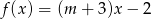 jest malejąca
jest malejąca
A) 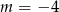 B)
B) 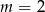 C)
C) 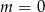 D)
D) 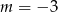
Promień okręgu o równaniu 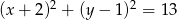 jest równy
jest równy
A) 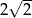 B)
B) 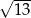 C) 13 D) 8
C) 13 D) 8
Ze zbioru liczb 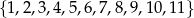 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 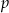 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 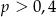 B)
B) 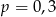 C)
C) 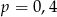 D)
D) 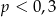
Mniejszą z dwóch liczb spełniających równanie 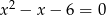 jest
jest
A) -2 B) -1 C) -3 D) -6
Wierzchołek paraboli będącej wykresem funkcji 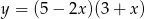 ma współrzędne
ma współrzędne
A) 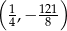 B)
B) 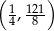 C)
C) 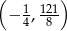 D)
D) 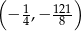
Dany jest nieskończony ciąg geometryczny 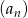 , w którym
, w którym 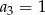 i
i 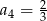 . Wtedy
. Wtedy
A) 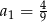 B)
B) 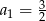 C)
C) 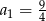 D)
D) 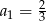
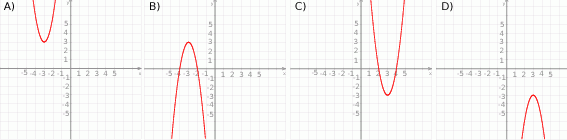
Zbiorem wartości funkcji kwadratowej 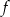 jest przedział
jest przedział 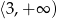 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji  ?
?
Która z podanych prostych jest symetryczna do prostej 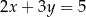 względem osi
względem osi 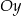 ?
?
A) 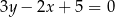 B)
B) 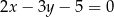 C)
C) 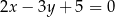 D)
D) 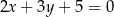
Pierwiastkami wielomianu stopnia trzeciego 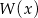 są liczby 2,-1,-3, a współczynnik stojący przy najwyższej potędze zmiennej
są liczby 2,-1,-3, a współczynnik stojący przy najwyższej potędze zmiennej  jest równy 4. Wielomian ten można zapisać w postaci
jest równy 4. Wielomian ten można zapisać w postaci
A) 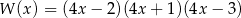
B) 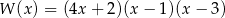
C) 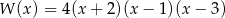
D) 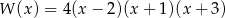
W trapezie prostokątnym kąt ostry ma miarę 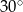 , a podstawy mają długości 8 i 10. Wysokość tego trapezu jest równa
, a podstawy mają długości 8 i 10. Wysokość tego trapezu jest równa
A) 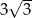 B) 4 C)
B) 4 C) 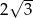 D)
D) 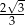
Po usunięciu jednej liczby z listy danych: 3,2,4,1,5,1,4,1,5,2 średnia arytmetyczna zwiększyła się o 0,2. Którą liczbę usunięto z listy?
A) 1 B) 4 C) 3 D) 2
Kąt  jest ostry i
jest ostry i 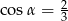 . Wartość wyrażenia
. Wartość wyrażenia 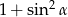 jest równa
jest równa
A)  B)
B)  C)
C) 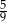 D)
D) 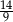
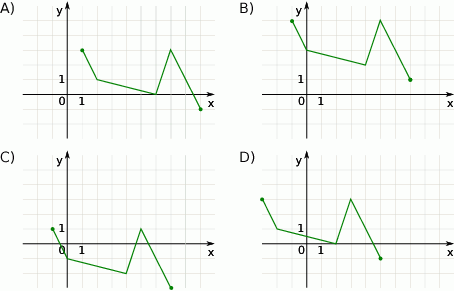
Rysunek przedstawia wykres funkcji 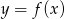 .
.
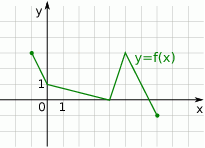
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 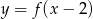 .
.
W kwadracie 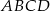 o boku długości 20 połączono punkty
o boku długości 20 połączono punkty 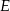 i
i 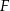 na bokach
na bokach 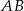 i
i 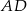 w ten sposób, że odcinek
w ten sposób, że odcinek 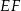 jest równoległy do przekątnej
jest równoległy do przekątnej 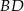 i jest od niej 5 razy krótszy.
i jest od niej 5 razy krótszy.
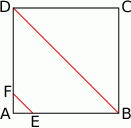
Długość odcinka 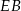 jest równa
jest równa
A) 14 B) 15 C) 12 D) 16
Przekątna prostopadłościanu o wymiarach 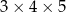 ma długość
ma długość
A) 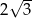 B)
B) 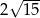 C)
C) 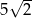 D)
D) 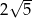
Dwa przeciwległe wierzchołki prostokąta mają współrzędne 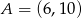 i
i 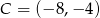 . Środek okręgu opisanego na tym prostokącie leży na prostej
. Środek okręgu opisanego na tym prostokącie leży na prostej
A) 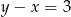 B)
B) 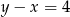 C)
C) 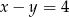 D)
D) 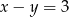
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 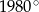 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 12 B) 9 C) 7 D) 13
Ile jest liczb naturalnych dwucyfrowych mniejszych od 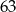 , które mają dwie różne cyfry?
, które mają dwie różne cyfry?
A) 45 B) 63 C) 58 D) 48
Układem sprzecznym jest układ
A) 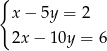 B)
B) 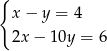 C)
C) 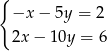 D)
D) 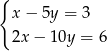
Suma współczynników wielomianu 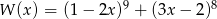 (po uporządkowaniu) jest równa
(po uporządkowaniu) jest równa
A) 3 B) 0 C) 2 D) 1
Punkty 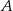 oraz
oraz 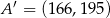 są symetryczne względem prostej
są symetryczne względem prostej 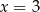 . Wówczas
. Wówczas
A) 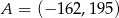 B)
B) 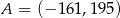 C)
C) 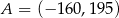 D)
D) 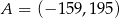
Rozwiąż nierówność 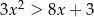 .
.
Rozwiąż równanie 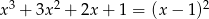 .
.
Suma trzech początkowych wyrazów ciągu geometrycznego wynosi 26, różnica wyrazów czwartego i pierwszego wynosi 52. Oblicz piąty wyraz tego ciągu.
W wazonie stoi 12 czerwonych i 8 żółtych róż. Pani Krystyna wyjęła losowo dwie róże z wazonu. Oblicz prawdopodobieństwo, że wśród wybranych kwiatów jest przynajmniej jedna róża żółta.
Oblicz 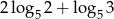 .
.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 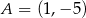 oraz
oraz 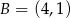 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 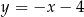 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Wyznacz współrzędne punktu 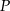 , który dzieli odcinek o końcach
, który dzieli odcinek o końcach 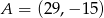 i
i 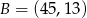 w stosunku
w stosunku 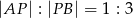 .
.
Podstawą graniastosłupa jest trójkąt prostokątny równoramienny o ramieniu długości 9. Kąt między przekątną największej ściany bocznej i wysokością graniastosłupa jest równy 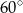 . Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
. Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.

