Zestaw użytkownika nr 2864_1923
sprawdzian z 1. semestru klasy 2 rozsz
Wskaż, który zbiór przedstawiony na osi liczbowej jest zbiorem liczb spełniających jednocześnie następujące nierówności: 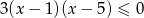 i
i 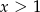 .
.

Liczb pierwszych należących do przedziału będącego rozwiązaniem nierówności 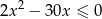 jest
jest
A) 7 B) nieskończenie wiele C) 6 D) 5
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 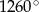 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 10 B) 11 C) 7 D) 9
Liczba przekątnych wielokąta wypukłego jest 5 razy większa od liczby jego boków. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 14 B) 10 C) 11 D) 13
Oblicz długość odcinka 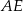 wiedząc, że
wiedząc, że 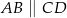 i
i 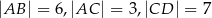 .
.
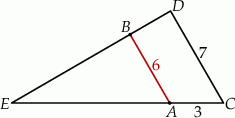
A) 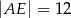 B)
B) 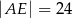 C)
C) 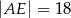 D)
D) 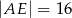
Dla jakich wartości parametru 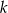 równanie
równanie 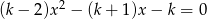 ma tylko ujemne rozwiązania?
ma tylko ujemne rozwiązania?
Dla jakich wartości parametru  równanie
równanie 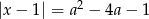 ma dwa dodatnie pierwiastki?
ma dwa dodatnie pierwiastki?
Zbadaj liczbę rozwiązań równania 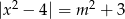 w zależności od parametru
w zależności od parametru 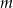 .
.
Znajdź taką wartość parametru 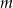 , aby największa wartość funkcji
, aby największa wartość funkcji 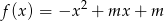 była najmniejsza z możliwych.
była najmniejsza z możliwych.
Funkcja kwadratowa 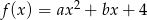 , osiąga wartości ujemne wtedy i tylko wtedy, gdy
, osiąga wartości ujemne wtedy i tylko wtedy, gdy 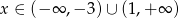 .
.
- Wyznacz wartości współczynników
 i
i 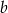 .
. - Napisz postać kanoniczną funkcji
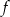 .
. - Podaj wzór funkcji kwadratowej
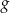 , której wykres otrzymamy przesuwając wykres funkcji
, której wykres otrzymamy przesuwając wykres funkcji 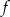 o wektor
o wektor ![→ u = [2,− 130]](https://img.zadania.info/zad/9353293/HzadT7x.gif) .
. - Wyznacz te argumenty
 , dla których
, dla których 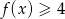 .
.
Wykres funkcji 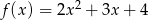 przesunięto o wektor
przesunięto o wektor ![→ v = [0,3]](https://img.zadania.info/zad/8939747/HzadT1x.gif) . Wyznacz wzór i narysuj wykres otrzymanej funkcji.
. Wyznacz wzór i narysuj wykres otrzymanej funkcji.
Zbadaj, na podstawie definicji, monotoniczność funkcji 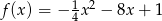 w zbiorze
w zbiorze 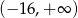 .
.
Pole trapezu prostokątnego opisanego na okręgu jest równe 5, a obwód trapezu wynosi 10. Oblicz długość promienia okręgu.
Ratownicy mający do dyspozycji linę o długości 80 metrów mają wytyczyć przy brzegu plaży kąpielisko w kształcie prostokąta (wzdłuż brzegu nie będzie liny). Jakie wymiary powinno mieć to kąpielisko, jeżeli wczasowicze chcą, aby miało ono jak największą powierzchnię? Należy przyjąć, że brzeg plaży tworzy linię prostą.
Większa część uczniów klasy liczącej 31 osób zachorowała na grypę. Zdrowi uczniowie postanowili wysłać chorym kolegom kartki z pozdrowieniami. Wiedząc, że każdy zdrowy uczeń wysłał do każdego chorego kolegi kartkę oraz, że liczba wysłanych kartek była największa z możliwych, oblicz ilu uczniów zachorowało na grypę.

