Zestaw użytkownika nr 2866_9275

sesja egzaminacyjnaklasa III gimnazjumczerwiec 2012Czas pracy: 60 min.Suma punktów: 24

Zadanie 1

(3 pkt)

Podstawą ostrosłupa prawidłowego jest kwadrat o przekątnej 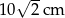√ -- 1 0 2 cm . Krawędź boczna ostrosłupa tworzy z podstawą kąt o mierze 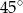45∘ . Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa.

Zadanie 2

(4 pkt)

Oblicz objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy 2 dm i krawędzi bocznej 4 dm.

Zadanie 3

(4 pkt)

Pole powierzchni czworościanu foremnego jest równe 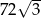√ -- 7 2 3 . Oblicz długość krawędzi tego czworościanu.

Zadanie 4

(3 pkt)

Suma wszystkich krawędzi ostrosłupa prawidłowego trójkątnego wynosi 72 cm. Oblicz długość krawędzi podstawy tego ostrosłupa, jeśli krawędź boczna ma długość 16 cm.

Zadanie 5

(4 pkt)

Jakie wielokąty mogą być podstawami ostrosłupa prawidłowego, w którym wszystkie krawędzie mają jednakową długość?

Zadanie 6

(1 pkt)

Zaznacz zdanie fałszywe.
A) Liczba wierzchołków każdego graniastosłupa jest liczbą parzystą.
B) Liczba krawędzi każdego graniastosłupa dzieli się przez 3.
C) Liczba krawędzi każdego ostrosłupa jest liczbą parzystą.
D) Liczba krawędzi każdego ostrosłupa dzieli się przez 3.

Zadanie 7

(5 pkt)

Rysunek przedstawia ostrosłup prosty.
Oceń, czy podane zdania są prawdziwe. Zaznacz TAK lub NIE.

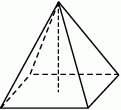
Ściany boczne ostrosłupa są trójkątami prostokątnymi.	TAK	NIE
Liczba wszystkich krawędzi ostrosłupa jest parzysta.	TAK	NIE
Wszystkie ściany boczne ostrosłupa mają wspólny wierzchołek.	TAK	NIE

Rozwiąż on-line Arkusz Wersja PDF