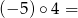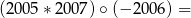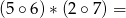Zestaw użytkownika nr 2880_5930

Zestaw użytkownika
nr 2880_5930

Zadanie 1

(2 pkt)

Oblicz miejsca zerowe funkcji

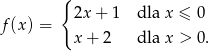
{ f(x) = 2x+ 1 dla x ≤ 0 x+ 2 dla x > 0 .

Zadanie 2

(3 pkt)

Dana jest funkcja 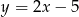y = 2x − 5 . Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor → v = [− 3,4] . Narysuj oba wykresy.

Zadanie 3

(5 pkt)

Dane są 4 liczby, z których 3 pierwsze tworzą ciąg geometryczny, a 3 ostatnie tworzą ciąg arytmetyczny. Suma pierwszej i czwartej wynosi 14, a suma drugiej i trzeciej wynosi 12. Znajdź te liczby.

Zadanie 4

(8 pkt)

Znajdź wielomian o współczynnikach całkowitych, którego pierwiastkiem jest liczba 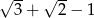√ -- √ -- 3+ 2− 1 .

Zadanie 5

(4 pkt)

Znajdź najmniejszą i największą wartość funkcji 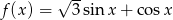√ -- f(x) = 3sinx + co sx w przedziale ⟨0 ;2π⟩ .

Zadanie 6

(5 pkt)

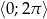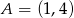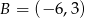Środek okręgu przechodzącego przez punkty A = (1,4) i B = (− 6,3 ) leży na osi .

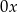Wyznacz równanie tego okręgu.
Wyznacz równanie prostej prostopadłej do prostej 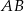i oddalonej od początku układu współrzędnych o .

Zadanie 7

(3 pkt)

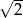Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia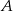
– na każdej kostce wypadła nieparzysta liczba oczek,
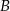– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 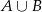A ∪ B .

Zadanie 8

(5 pkt)

Narysuj wykresy funkcji 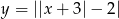oraz 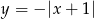, gdzie .
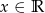Wyznacz te wartości parametru 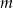, dla których równanie 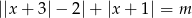ma dokładnie dwa rozwiązania.

Zadanie 9

(5 pkt)

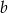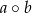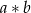Dla dowolnych liczb rzeczywistych i określamy liczby a ∘ b i a∗ b w następujący sposób:

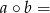liczba nie mniejsza spośród liczb i ,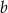
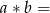liczba nie większa spośród liczb a i b.

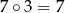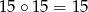Na przykład: 7 ∘3 = 7 , 15 ∘ 15 = 15 , 7∗ 3 = 3 , (− 6)∗ 4 = − 6 , (− 3) ∗(− 3) = −3 .
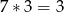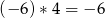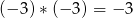Oblicz

Zadanie 10

(5 pkt)

Jaka jest wysokość budynku rzucającego cień długości 19 m w momencie, gdy promienie słoneczne padają pod kątem 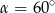α = 60∘ . Wynik podaj z dokładnością do 10 cm.

Zadanie 11

(5 pkt)

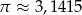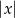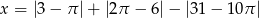Wiedząc, że π ≈ 3,1415 oblicz |x | , gdzie x = |3− π| + |2π − 6| − |31− 10π | .

Rozwiąż on-line Arkusz Wersja PDF