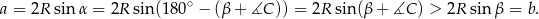Zadanie nr 2886102
Udowodnij, że jeżeli w trójkącie dwa kąty nie są równe, to naprzeciw większego z nich leży dłuższy bok.
Rozwiązanie
Szkicujemy trójkąt.
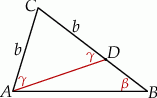
Oznaczmy podane kąty przez 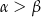 , a leżące naprzeciwko nich boki przez
, a leżące naprzeciwko nich boki przez  i
i 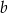 . Mamy pokazać, że
. Mamy pokazać, że 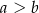 .
.
Sposób I
Jeżeli 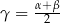 , to
, to
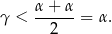
Możemy zatem znaleźć na boku 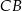 taki punkt
taki punkt 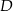 , że
, że 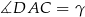 . Wtedy
. Wtedy
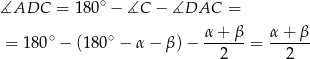
Zatem trójkat 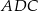 jest równoramienny i
jest równoramienny i 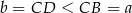 , co mieliśmy pokazać.
, co mieliśmy pokazać.
Sposób II
Jeżeli 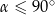 , to również
, to również 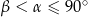 . Funkcja
. Funkcja 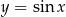 jest rosnąca w pierwszej ćwiartce, więc na mocy twierdzenia sinusów mamy
jest rosnąca w pierwszej ćwiartce, więc na mocy twierdzenia sinusów mamy
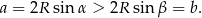
Jeżeli natomiast 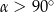 , to
, to 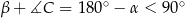 , więc podobnie jak poprzednio mamy
, więc podobnie jak poprzednio mamy