Zestaw użytkownika nr 2909_6536

Zestaw użytkownika
nr 2909_6536

Zadanie 1

Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma miarę 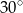30∘ . Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.

Zadanie 2

W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 18 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 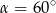α = 60∘ . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt .

Zadanie 3

Przekątna przekroju osiowego walca ma długość 5 cm i jest nachylona do płaszczyzny podstawy pod kątem 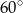60 ∘ . Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?

Zadanie 4

Przez środek jednej krawędzi podstawy sześcianu, koniec przeciwległej krawędzi tej podstawy oraz środek krawędzi bocznej, poprowadzono płaszczyznę. Opisz ﬁgurę, którą otrzymamy w wyniku tego przekroju. Rozważ 2 przypadki.

Zadanie 5

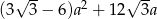Pole powierzchni całkowitej graniastosłupa prawidłowego sześciokątnego o krawędzi podstawy wyraża się wzorem √ -- √ -- (3 3 − 6)a2 + 12 3a . Wyznacz sumę długości krawędzi podstawy i wysokości tego graniastosłupa.

Zadanie 6

W ostrosłupie 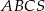ABCS podstawa 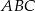ABC jest trójkątem prostokątnym, 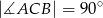|∡ACB | = 90∘ . Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10cm. Wysokość 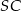ostrosłupa ma długość 24cm. Oblicz:

objętość ostrosłupa;
tangens kąta nachylenia ściany bocznej ostrosłupa, zawierającej przeciwprostokątną podstawy, do płaszczyzny podstawy.

Zadanie 7

Objętość graniastosłupa prawidłowego trójkątnego jest równa 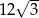√ -- 12 3 , a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.

Zadanie 8

Do naczynia w kształcie odwróconego stożka wrzucono kulkę o promieniu 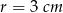r = 3 cm . Oceń, czy kulka będzie wystawać nad brzeg naczynia. Uzasadnij odpowiedź wykonując odpowiednie obliczenia, jeżeli wiadomo, że wysokość stożka wynosi 12 cm a promień podstawy 4 cm.

Zadanie 9

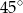Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa . Kąt między krawędzią boczną i krawędzią podstawy ma miarę 4 5∘ . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.

Zadanie 10

Podstawą ostrosłupa jest trójkąt prostokątny, którego kąt ostry ma miarę 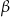. Wszystkie krawędzie boczne mają długość 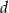i są nachylone do płaszczyzny podstawy pod kątem o mierze . Oblicz objętość tego ostrosłupa.

Arkusz Wersja PDF