Zestaw użytkownika nr 2933_1084
Zestaw użytkownika
nr 2933_1084
W tabeli zapisano cztery liczby.
| I | 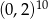 |
| II | 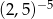 |
| III | 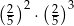 |
| IV | 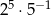 |
Liczba 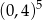 jest równa liczbom
jest równa liczbom
A) II i III B) III i IV C) I i III D) I i II E) II i IV
Dwudziestu sześciu uczniów klasy gimnazjalnej postanowiło wybrać się na czterodniową wycieczkę z trzema noclegami. Trasa przejazdu wynosiła łącznie 600 km. W biurze turystycznym uczniowie otrzymali następujące propozycje:
– cena jednego noclegu – 25 zł od osoby
– wyżywienie w ciągu jednego dnia (śniadanie, obiad, kolacja) – 30 zł od osoby
– bilety wejściowe do muzeum i przewodnik grupy dla całej wycieczki – 1200 zł
– cena 1 km przejazdu autokarem – 2,50 zł
Oblicz łączny koszt wycieczki dla całej grupy, jeśli pierwszego dnia uczniowie mają zamiar skorzystać tylko z obiadu i kolacji, czwartego dnia tylko ze śniadania. Oblicz koszt wycieczki na jednego ucznia.
Album do zdjęć ma 21 stron. W albumie są 63 zdjęcia. Na każdej stronie jest taka sama liczba zdjęć. Które wyrażenie opisuje liczbę zdjęć znajdujących się na jednej stronie albumu?
A) 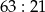 B)
B) 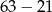 C)
C) 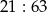 D)
D) 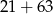
Największy wspólny dzielnik liczb 120 i 180, to
A) 20 B) 60 C) 90 D) 30
W pierwszym miesiącu wydawnictwo sprzedawało książkę po cenie 20 zł. W drugim miesiącu cenę obniżono o 10%, co spowodowało wzrost przychodów o 8%. O ile procent więcej książek sprzedano w drugim miesiącu niż w pierwszym?
Uczeń przeczytał w ciągu tygodnia książkę liczącą 420 stron.
| Dzień | Liczba przeczytanych stron | Czas czytania |
| 1. | 50 | 1 h 40 min |
| 2. | 70 | 2 h |
| 3. | 90 | 2 h 20 min |
| 4. | 30 | 30 min |
| 5. | 70 | 2 h 10 min |
| 6. | 80 | 2 h 30 min |
| 7. | 30 | 30 min |
Na podstawie informacji zawartych w powyższej tabeli wybierz zdanie prawdziwe.
A) Pierwszego dnia uczeń przeczytał ponad 20% całej książki.
B) Uczeń czytał średnio 50 stron dziennie.
C) Piątego dnia uczeń przeczytał 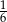 całej książki.
całej książki.
D) Przeczytanie pierwszej połowy książki zajęło uczniowi mniej czasu niż przeczytanie drugiej połowy.
Rozmiar ramy roweru to długość fragmentu rury pod siodełkiem mierzona tak, jak przedstawiono na rysunku – od środka miejsca, w którym obracają się pedały do środka rury łączącej siodełko z kierownicą.
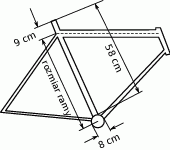
Jaki jest rozmiar ramy, której niektóre wymiary przedstawiono na rysunku?
A) 58 cm B) 53 cm C) 59 cm D) 49 cm
Do przygotowania podwieczorku użyto 120 mandarynek i 180 śliwek. Każda porcja składała się z takiej samej liczby mandarynek i takiej samej liczby śliwek, a owoców nie dzielono na części.
Dla ilu maksymalnie osób przygotowano taki podwieczorek?
A) 20 B) 30 C) 90 D) 60
Wykaż, że suma pięciu kolejnych liczb naturalnych nie może być liczbą pierwszą.
Uprość wyrażenie 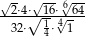 .
.
Oblicz 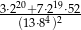 .
.
Wykaż, że iloczyn trzech kolejnych liczb podzielnych przez 3 dzieli się przez 81.
Stężenie pewnego roztworu wodnego soli wynosi 5%. Ile kilogramów czystej wody należy dodać do 90 kg tego roztworu, aby otrzymać roztwór o stężeniu 2%?
Oblicz: 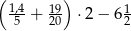 .
.
Wykaż, że liczba 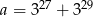 jest podzielna przez 30.
jest podzielna przez 30.
Liczba 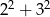 jest równa
jest równa
A) 36 B) 13 C) 10 D) 25
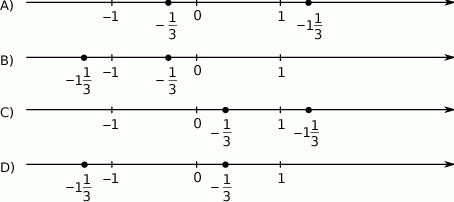
Na której osi liczbowej prawidłowo zaznaczono liczby 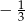 i
i 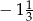 ?
?
Znajdź liczbę, której 37% wynosi: 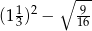 .
.
Janek ma 39 znaczków pocztowych w jednej kopercie i 16 w drugiej i chce dołożyć do każdej koperty tyle samo znaczków w tym celu, żeby w pierwszej było 2 razy więcej znaczków niż w drugiej. Po ile znaczków powinien dołożyć do każdej koperty?
Liczbę 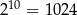 możemy przybliżyć tak:
możemy przybliżyć tak: 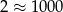 , a liczbę
, a liczbę 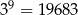 tak:
tak: 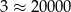 . To pozwala przybliżać inne liczby, na przykład
. To pozwala przybliżać inne liczby, na przykład 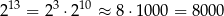 .
.
Wykorzystując podane przybliżenia liczb 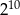 oraz
oraz 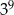 , wybierz najlepsze przybliżenie liczb
, wybierz najlepsze przybliżenie liczb 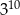 ,
, 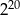 oraz
oraz 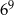 .
.
| Potęga | Propozycje przybliżeń | ||
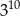 | A) 30 000 | B) 60 000 | C) 200 000 |
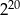 | A) 2 000 | B) 4 000 | C) 1 000 000 |
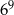 | A) 15 000 | B) 40 000 | C) 10 000 000 |
VAT to podatek doliczany do cen towarów i usług. Cena powiększona o doliczony podatek VAT nazywana jest ceną brutto. W pewnym sklepie stawka VAT na wszystkie towary wynosi 22%.
Jeśli znamy cenę brutto towaru z tego sklepu, to aby obliczyć jego cenę bez podatku, wystarczy
| od ceny brutto odjąć jej 22% | TAK | NIE |
| podzielić cenę brutto przez 1,22 | TAK | NIE |
| obliczyć 78% ceny brutto | TAK | NIE |
| pomnożyć cenę brutto przez 100 i wynik podzielić przez 122 | TAK | NIE |
| podzielić cenę brutto przez 0,78 | TAK | NIE |
Wykaż, że 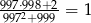 .
.
Stężenie roztworu kwasu solnego wynosi 5%. Ile kilogramów wody należy dodać do 44 kg tego roztworu, aby stężenie roztworu zmniejszyło się do 2%?
Oblicz odwrotność liczby 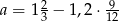 .
.
Które zdanie jest fałszywe?
A) Suma kolejnych dwóch liczb naturalnych jest liczbą nieparzystą.
B) Iloczyn kolejnych dwóch liczb naturalnych jest liczbą parzystą.
C) Różnica dwóch liczb nieparzystych jest liczbą nieparzystą.
D) Suma dwóch liczb nieparzystych jest liczbą parzystą.

