Zestaw użytkownika nr 2951_1540
Sprawdzian Wielomiany gr ASuma punktów: 22
Wartość wielomianu 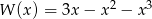 dla
dla 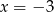 jest równa
jest równa
A) 12 B) -9 C) 9 D) -24
Stopień wielomianu 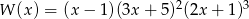 jest równy
jest równy
A) 4 B) 5 C) 6 D) 8
Wiadomo, że 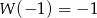 , gdy
, gdy 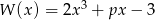 . Zatem wartość współczynnika
. Zatem wartość współczynnika 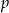 wynosi:
wynosi:
A) 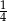 B) -4 C) 4 D) -1
B) -4 C) 4 D) -1
Dane są wielomiany 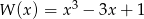 oraz
oraz 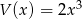 . Wielomian
. Wielomian 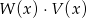 jest równy
jest równy
A) 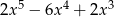 B)
B) 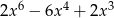 C)
C) 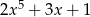 D)
D) 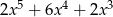
Pierwiastkami wielomianu stopnia trzeciego 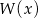 są liczby
są liczby 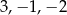 , a współczynnik stojący przy najwyższej potędze zmiennej
, a współczynnik stojący przy najwyższej potędze zmiennej  jest równy 3. Wielomian ten można zapisać w postaci
jest równy 3. Wielomian ten można zapisać w postaci
A) 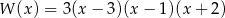
B) 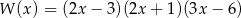
C) 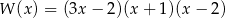
D) 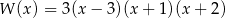
Suma pierwiastków wielomianu 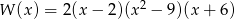 jest równa
jest równa
A) 5 B) 8 C) 4 D) -4
Liczba pierwiastków wielomianu 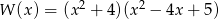 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Pierwiastkami równania 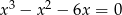 są liczby
są liczby
A) 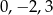 B)
B) 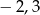 C)
C) 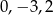 D)
D) 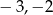
Liczba 3 jest pierwiastkiem wielomianu 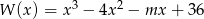 . Wyznacz parametr
. Wyznacz parametr 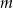 i pozostałe pierwiastki tego wielomianu.
i pozostałe pierwiastki tego wielomianu.
Rozwiąż równanie 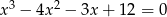 .
.
Rozłóż wielomian 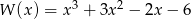 na czynniki liniowe.
na czynniki liniowe.
Wielomiany 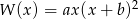 i
i 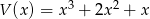 są równe. Oblicz
są równe. Oblicz  i
i 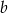 .
.

