Zestaw użytkownika nr 2952_7319

matura próbna rozszerzona z funkcji 2

Zadanie 1
(5 pkt)

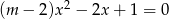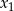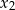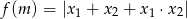Różnymi pierwiastkami równania kwadratowego 2 (m − 2)x − 2x + 1 = 0 są liczby x1 oraz x2 . Narysuj wykres funkcji f (m) = |x 1 + x 2 + x 1 ⋅x2| .

Zadanie 2
(5 pkt)

Wyznacz wszystkie wartości parametru 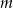m , dla których równanie 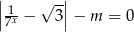| √ --| || 1x − 3 ||− m = 0 7 ma dwa pierwiastki, których iloczyn jest ujemny.

Zadanie 3
(5 pkt)

Dany jest wielomian 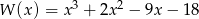3 2 W (x) = x + 2x − 9x − 18 .

  • Wyznacz pierwiastki tego wielomianu.
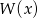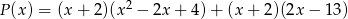  • Sprawdź, czy wielomiany W (x ) i P(x ) = (x+ 2)(x2 − 2x + 4) + (x + 2)(2x − 1 3) są równe.
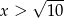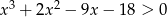  • Uzasadnij, że jeśli √ --- x > 10 , to 3 2 x + 2x − 9x − 18 > 0 .
Zadanie 4
(5 pkt)

Znajdź te wartości parametru 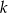k , dla których zbiorem rozwiązań nierówności 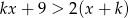kx + 9 > 2(x + k) jest przedział (− ∞ ;3) .

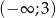Zadanie 5
(5 pkt)

Dla każdej liczby 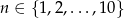n ∈ { 1,2,...,10} tworzymy funkcję 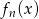fn(x) , której wykres powstaje przez przesunięcie wykresu funkcji 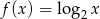f(x ) = lo g2x o wektor [0,−n ] .

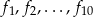  • Oblicz sumę wszystkich miejsc zerowych funkcji f ,f ,...,f 1 2 10 .
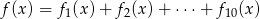  • Wyznacz miejsce zerowe funkcji f(x) = f1(x)+ f2(x)+ ⋅⋅⋅+ f10(x) .
Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze