Zestaw użytkownika nr 3016_3086
Zestaw użytkownika
nr 3016_3086
Oblicz najmniejszą i największą wartość funkcji kwadratowej 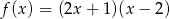 w przedziale
w przedziale 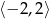 .
.
Wyznacz wzór funkcji 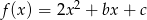 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 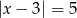 .
.
Wyznacz najmniejszą i największą wartość funkcji 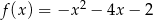 w przedziale
w przedziale 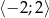 .
.
Wyznacz największą i najmniejszą wartość funkcji 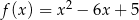 osiąganą w przedziale
osiąganą w przedziale 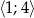 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 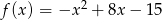 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 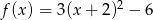 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 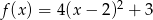 .
.
Dla jakich wartości parametru 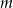 funkcja
funkcja 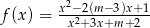 jest określona dla każdego
jest określona dla każdego 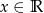 i ma dwa różne miejsca zerowe?
i ma dwa różne miejsca zerowe?
Określ dziedzinę funkcji 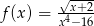 .
.
Wyznacz największą wartość funkcji 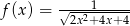 .
.
Wyznacz najmniejszą i największą wartość funkcji 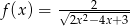 na przedziale
na przedziale 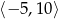 .
.
Wyznacz dziedzinę funkcji  .
.
Wyznacz dziedzinę funkcji 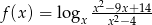 .
.
Wyznacz dziedzinę funkcji 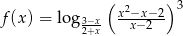
Wyznacz miejsca zerowe funkcji
Funkcja 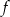 jest określona wzorem
jest określona wzorem
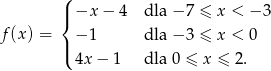
- Podaj dziedzinę funkcji
 .
. - Podaj jej miejsca zerowe.
- Naszkicuj wykres tej funkcji.
- Podaj zbiór wartości funkcji
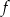 .
.

