Zestaw użytkownika nr 3073_3868
Zestaw użytkownika
nr 3073_3868
Ze zbioru liczb 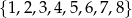 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 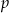 jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
A) 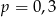 B)
B) 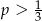 C)
C) 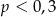 D)
D) 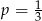
Średnia arytmetyczna pięciu liczb: 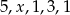 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 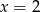 B)
B) 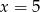 C)
C) 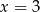 D)
D) 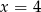
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 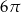 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 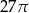 B)
B) 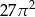 C)
C) 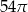 D)
D) 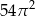
Na loterii jest 10 losów, z których 4 są wygrywające. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A)  B)
B)  C)
C)  D)
D) 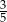
Z talii 52 kart losujemy jedną. Prawdopodobieństwo, że wylosujemy króla lub kiera, jest równe
A) 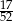 B)
B) 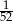 C)
C) 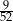 D)
D) 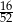
Powierzchnia sześcianu wynosi 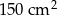 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 5,5 cm B) 4 cm C) 6 cm D) 5 cm
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sumy oczek równej trzy wynosi
A) 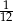 B)
B) 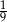 C)
C)  D)
D) 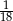
O zdarzeniach losowych 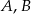 wiadomo, że:
wiadomo, że: 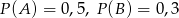 i
i 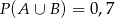 . Prawdopodobieństwo iloczynu zdarzeń
. Prawdopodobieństwo iloczynu zdarzeń 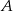 i
i 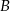 spełnia warunek
spełnia warunek
A) 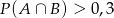 B)
B) 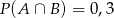 C)
C) 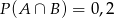 D)
D) 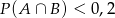
Mediana danych: 0, 1, 1, 2, 3, 1 jest równa
A) 2 B) 2,5 C) 1 D) 1,5
Krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość 7, a krawędź podstawy ma długość 8. Wysokość tego ostrosłupa jest równa
A) 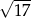 B) 5 C) 9 D)
B) 5 C) 9 D) 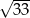
Kula ma objętość 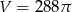 . Promień
. Promień  tej kuli jest równy
tej kuli jest równy
A) 8 B) 12 C) 9 D) 6
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są mniejsze od 5 jest
A) 30 B) 20 C) 25 D) 16
Podstawą ostrosłupa jest prostokąt o bokach 6cm i 8cm. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod katem 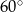 . Oblicz pole powierzchni ostrosłupa.
. Oblicz pole powierzchni ostrosłupa.
W koszu znajdują się owoce: 12 jabłek i 8 pomarańczy. Wyjmujemy kolejno trzy owoce, nie odkładając ich do kosza. Jakie jest prawdopodobieństwo, że wylosujemy dokładnie dwie pomarańcze.
Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna ma długość 18 cm i tworzy z bokiem odpowiadającym wysokości walca kąt o mierze 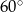 . Oblicz objętość walca.
. Oblicz objętość walca.
Tabela przedstawia pewne dane i ich liczebność
| Wartość danej | -4 | 2 | 4 | 7 | 20 |
| Liczebność | 7 | 2 | 3 | 6 | 2 |
- Oblicz średnią arytmetyczną tych danych.
- Podaj medianę.
- Oblicz odchylenie standardowe.

