Zestaw użytkownika nr 3117_3581

Egzamin klasyfikacyjnysemestr drugi klasa I PR16 Czerwca 2011Suma punktów: 35

Zadanie 1
(5 pkt)

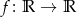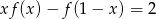Znajdź wszystkie funkcje f : R → R , dla których zachodzi równość xf (x)− f(1 − x) = 2 .

Zadanie 2
(5 pkt)

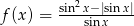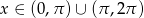Dana jest funkcja f określona wzorem sin2x−|sinx|- f(x) = sin x dla x ∈ (0,π) ∪ (π ,2 π) .

  • Naszkicuj wykres funkcji f .
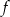  • Wyznacz miejsca zerowe funkcji f .
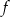Zadanie 3
(5 pkt)

Narysuj wykres funkcji 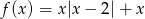f (x) = x|x − 2|+ x , gdzie 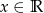x ∈ R i na jego podstawie odpowiedź na pytania.

  • Jaki jest zbiór wartości funkcji?
  • Dla jakich argumentów wartość funkcji wynosi 2?
  • W jakich przedziałach funkcja jest rosnąca?
  • Czy funkcja jest parzysta?
Zadanie 4
(5 pkt)

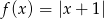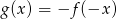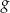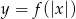Korzystając z wykresu funkcji f(x ) = |x+ 1| wykonaj takie przekształcenia aby otrzymać krzywe o równaniach y = −f (−x ) , y = f(x − 3) + 2 i y = f(|x|) . Zapisz równania otrzymanych krzywych.

Zadanie 5
(5 pkt)

Dany jest trójkąt 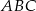ABC o wierzchołkach A = (1;4) , B = (5;2) , C = (3 ;− 3 ) .

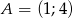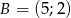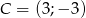  • Napisz równanie wysokości opuszczonej z wierzchołka 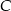C na bok AB .
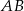  • Napisz równanie środkowej boku BC .
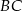  • Napisz równanie symetralnej boku BC .
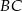  • Oblicz obwód i pole tego trójkąta.
Zadanie 6
(5 pkt)

Dany jest trójkąt 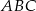ABC o wierzchołkach A = (1;4) , B = (5;2) , C = (3 ;− 3 ) .

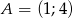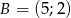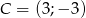  • Napisz równanie wysokości opuszczonej z wierzchołka 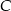C na bok AB .
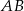  • Napisz równanie środkowej boku BC .
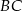  • Napisz równanie symetralnej boku BC .
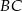  • Oblicz obwód i pole tego trójkąta.
Zadanie 7
(5 pkt)

Oblicz pole i obwód trójkąta o wierzchołkach: 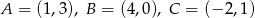A = (1,3), B = (4,0), C = (− 2,1) .

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze