Zestaw użytkownika nr 3157_8300

Zestaw użytkownika
nr 3157_8300

Zadanie 1

Wyznacz najmniejszą i największą wartość funkcji 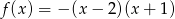f(x) = −(x − 2 )(x+ 1) w przedziale ⟨0 ;4⟩ .

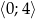Zadanie 2

Określ dziedzinę funkcji 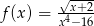√x+-2 f(x) = x4− 16 .

Zadanie 3

Wyznacz wzór funkcji 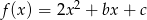2 f (x ) = 2x + bx + c w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania |x − 3| = 5 .

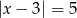Zadanie 4

Wyznacz miejsca zerowe funkcji

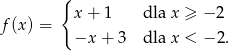
{ f (x) = x + 1 dla x ≥ − 2 −x + 3 dla x < − 2.

Zadanie 5

Dany jest wielomian 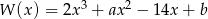3 2 W (x) = 2x + ax − 14x+ b .

Dla 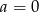i 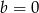otrzymamy wielomian 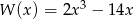. Rozwiąż równanie .
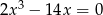Dobierz wartości i 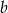tak, aby wielomian 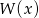był podzielny jednocześnie prze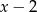z oraz .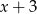

Zadanie 6

Wiadomo, że funkcja liniowa 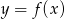y = f(x) przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy 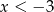x < − 3 . Ponadto, 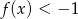f (x) < − 1 wtedy i tylko wtedy, gdy 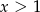x > 1 . Wyznacz wzór funkcji .

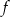Zadanie 7

Dzienny dochód hurtowni akumulatorów wyraża się wzorem 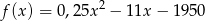f (x) = 0,25x 2 − 11x − 1950 , gdzie oznacza liczbę sprzedanych akumulatorów.

Oblicz przy jakiej liczbie sprzedanych akumulatorów ﬁrma poniesie największą stratę. Oblicz wartość tej straty.
Oblicz ile akumulatorów należy sprzedać, aby dzienny dochód wynosił 4985.

Zadanie 8

Samochód przebył w pewnym czasie 210 km. Gdyby jechał ze średnią prędkością o 10 km/h większą, to czas przejazdu skróciłby się o pół godziny. Oblicz, z jaką średnią prędkością jechał ten samochód.

Arkusz Wersja PDF