Zestaw użytkownika nr 3214_9450
Zestaw użytkownika
nr 3214_9450
Wiadomo, że funkcja liniowa 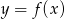 przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy
przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy 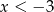 . Ponadto,
. Ponadto, 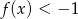 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 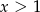 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 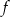 .
.
Kąta  jest ostry oraz
jest ostry oraz 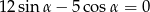 . Oblicz
. Oblicz 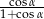 .
.
Dla jakich wartości parametru  reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 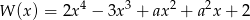 przez dwumian
przez dwumian 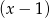 jest większa od 3.
jest większa od 3.
Uzasadnij, że dla każdej liczby naturalnej  wartość wielomianu
wartość wielomianu 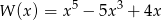 jest liczbą podzielną przez 120.
jest liczbą podzielną przez 120.
Funkcja liniowa 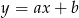 jest malejąca i jej miejscem zerowym jest liczba niedodatnia. Ustal znak wyrażenia
jest malejąca i jej miejscem zerowym jest liczba niedodatnia. Ustal znak wyrażenia 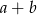 .
.
Miejscami zerowymi funkcji kwadratowej 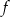 są liczby (-6) oraz 1. Oblicz wartość wyrażenia
są liczby (-6) oraz 1. Oblicz wartość wyrażenia 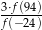 .
.
Funkcja 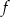 określona wzorem
określona wzorem 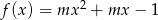 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 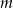 , dla których:
, dla których:
- funkcja
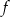 przyjmuje tylko wartości ujemne,
przyjmuje tylko wartości ujemne, - zbiorem wartości funkcji
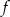 jest przedział
jest przedział 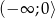 .
.
Wyznacz wartości  i
i 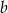 współczynników wielomianu
współczynników wielomianu 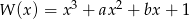 wiedząc, że
wiedząc, że 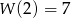 oraz, że reszta z dzielenia
oraz, że reszta z dzielenia 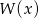 przez
przez 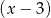 jest równa 10.
jest równa 10.
Wyznacz dziedzinę funkcji  .
.
Funkcja liniowa 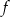 określona jest wzorem
określona jest wzorem 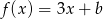 , dla
, dla 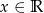 . Wyznacz współczynnik
. Wyznacz współczynnik 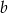 , wiedząc, że
, wiedząc, że 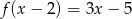 .
.
Dla każdej liczby rzeczywistej  obliczamy różnicę sześcianów liczb: o 1 mniejszej od
obliczamy różnicę sześcianów liczb: o 1 mniejszej od  oraz o 2 większej od
oraz o 2 większej od  . Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
. Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
Wyznacz współczynniki funkcji kwadratowej 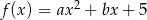 wiedząc, że
wiedząc, że 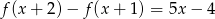 .
.
Wyznacz dziedzinę funkcji 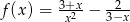 .
.
Z równania 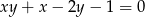 wyznacz
wyznacz 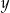 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz jej dziedzinę oraz współrzędne punktów przecięcia wykresu z osiami układu współrzędnych.
. Wyznacz jej dziedzinę oraz współrzędne punktów przecięcia wykresu z osiami układu współrzędnych.
Określ dziedzinę funkcji 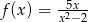 .
.
Sprawdź, czy równe są wielomiany 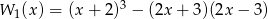 i
i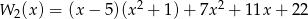 .
.
Kąt  jest ostry i
jest ostry i 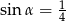 . Oblicz
. Oblicz 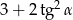 .
.
Reszta z dzielenia wielomianu 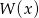 przez wielomian
przez wielomian 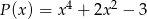 jest wielomianem
jest wielomianem 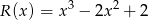 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 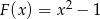 .
.
W wyniku podzielenia wielomianu 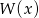 przez
przez 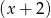 otrzymujemy iloraz
otrzymujemy iloraz 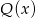 i resztę 0. Jeśli natomiast podzielimy wielomian
i resztę 0. Jeśli natomiast podzielimy wielomian 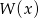 przez
przez 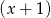 , to otrzymamy iloraz
, to otrzymamy iloraz 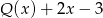 i resztę 2.
i resztę 2.
- Wyznacz wielomian
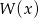 .
. - Rozwiąż nierówność
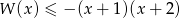 .
.
Wielomian 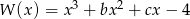 jest podzielny przez trójmian kwadratowy
jest podzielny przez trójmian kwadratowy 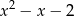 . Wyznacz współczynniki
. Wyznacz współczynniki 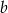 i
i  wielomianu
wielomianu 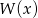 .
.

