Zestaw użytkownika nr 3215_6188
Zestaw użytkownika
nr 3215_6188
W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu opisanego ma długość 19 cm. Oblicz pole tego trójkąta.
Na bokach 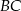 i
i 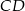 równoległoboku
równoległoboku 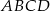 zbudowano kwadraty
zbudowano kwadraty 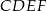 i
i  (zobacz rysunek).
(zobacz rysunek).
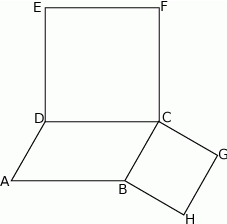
Udowodnij, że 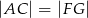 .
.
W trapezie równoramiennym przekątna ma długość 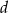 i tworzy z dłuższą podstawą kąt o mierze
i tworzy z dłuższą podstawą kąt o mierze  . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu.
Miary kątów trójkąta są w stosunku 1:2:3. Obwód koła opisanego na tym trójkącie jest równy 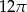 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
W trójkącie prostokątnym dany jest kąt ostry o mierze  i pole
i pole 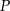 tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
W trapezie kąty przy dłuższej podstawie to 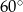 i
i 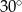 , a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.
, a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.
Stosunek długości przekątnych rombu o boku 17 cm jest równy 5:3. Oblicz pole rombu.
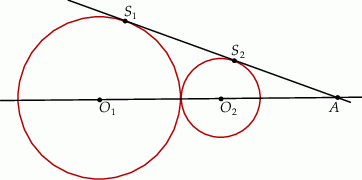
Dane są 2 koła styczne zewnętrznie o promieniach 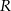 i
i  (
(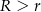 ) oraz środkach
) oraz środkach 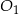 i
i 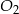 . Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach
. Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach 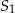 i
i 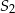 odpowiednio (
odpowiednio (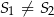 ). Oblicz pole trójkąta
). Oblicz pole trójkąta 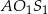 , gdzie
, gdzie 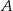 jest punktem przecięcia się prostych
jest punktem przecięcia się prostych 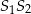 i
i 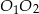 .
.
Dany jest trójkąt prostokątny 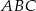 , w którym
, w którym 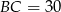 ,
, 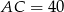 i
i 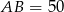 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 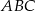 jest styczny do boku
jest styczny do boku 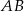 w punkcie
w punkcie 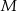 . Oblicz długość odcinka
. Oblicz długość odcinka 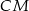 .
.
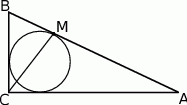
W trójkącie równoramiennym 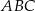 o kącie przy wierzchołku
o kącie przy wierzchołku 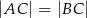 poprowadzono wysokość
poprowadzono wysokość 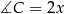 . Wiedząc, że
. Wiedząc, że 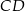 oblicz odległość środków okręgów wpisanych w trójkąty
oblicz odległość środków okręgów wpisanych w trójkąty 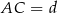 i
i 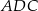 .
.
Pole rombu jest równe 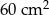 . Dłuższa przekątna rombu podzieliła kąt ostry rombu na takie dwa kąty o mierze
. Dłuższa przekątna rombu podzieliła kąt ostry rombu na takie dwa kąty o mierze  , że
, że 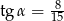 . Oblicz długość boku rombu.
. Oblicz długość boku rombu.
Miara kąta między ramionami trójkąta równoramiennego o polu 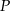 jest równa
jest równa  . Oblicz promień okręgu wpisanego w ten trójkąt.
. Oblicz promień okręgu wpisanego w ten trójkąt.
Czworokąt 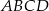 jest wpisany w okrąg. Dane są
jest wpisany w okrąg. Dane są 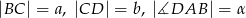 . Wyznacz długość przekątnej
. Wyznacz długość przekątnej 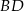 .
.
Do dwóch okręgów o promieniach długości 3cm i 10cm poprowadzono wspólną styczną tak, że okręgi znajdują się po różnych stronach tej stycznej. Odległość między środkami okręgów wynosi 39 cm. Oblicz długość odcinka między punktami styczności.
Suma długości dwóch boków trójkąta wynosi 6 cm, a miara kąta pomiędzy tymi bokami wynosi 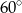 . Jaką najmniejszą wartość ma obwód tego trójkąta.
. Jaką najmniejszą wartość ma obwód tego trójkąta.
W trapezie równoramiennym długość krótszej podstawy wynosi 9 cm, przekątnej 17 cm a ramienia 10 cm. Oblicz jego pole.
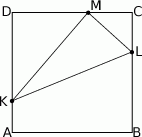
Na bokach 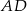 ,
, 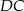 i
i 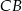 kwadratu
kwadratu 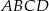 wybrano punkty
wybrano punkty 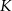 ,
, 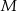 i
i 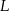 ten sposób, że
ten sposób, że 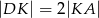 ,
, 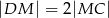 , oraz
, oraz 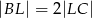 .
.
- Uzasadnij, że trójkąt
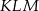 jest prostokątny.
jest prostokątny. - Oblicz tangensy kątów ostrych trójkąta
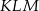 .
.
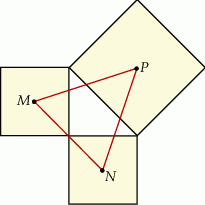
Na zewnątrz równoramiennego trójkąta prostokątnego o przyprostokątnych równych  zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt
zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt 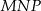 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 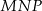 jest równe
jest równe 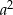 .
.
Dany jest prostokąt 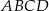 , którego boki mają długości
, którego boki mają długości  i
i 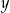 . Punkt
. Punkt 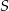 jest punktem przecięcia się przekątnych prostokąta.
jest punktem przecięcia się przekątnych prostokąta.
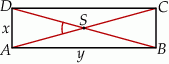
- Wykaż, że pole trójkąta
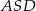 jest cztery razy mniejsze od pola prostokąta
jest cztery razy mniejsze od pola prostokąta 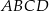 .
. - Wiedząc dodatkowo, że
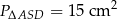 i
i 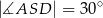 , oblicz pole kwadratu, którego bok ma długość
, oblicz pole kwadratu, którego bok ma długość 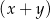 .
.

