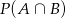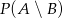Zestaw użytkownika nr 3320_3472

Zestaw użytkownika
nr 3320_3472

Zadanie 1

Rzucamy sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że wypadną co najmniej dwa oczka.

Zadanie 2

Rzucamy trzy razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 12.

Zadanie 3

W pudełku zmieszano 30 ziaren fasoli, 20 ziaren ciecierzycy i 50 ziaren grochu.

Losujemy jedno ziarenko. Jakie jest prawdopodobieństwo wylosowania ziarenka ciecierzycy?
Jako pierwsze wylosowano ziarenko fasoli. Jakie jest prawdopodobieństwo, że drugim wylosowanym ziarenkiem nie będzie ziarenko fasoli?
Z pudełka usunięto po 10% ziarenek każdego rodzaju. Jakie jest prawdopodobieństwo wylosowania ziarenka fasoli?

Zadanie 4

W urnie znajduje się 5 kul białych, 3 kule czerwone i 1 zielona. Losujemy 1 kulę. Oblicz prawdopodobieństwo wylosowania kuli białej.

Zadanie 5

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo każdego z następujących zdarzeń:

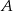— w każdym rzucie wypadnie nieparzysta liczba oczek.
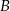-– suma oczek otrzymanych w obu rzutach jest liczbą większą od 9.
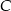-– suma oczek otrzymanych w obu rzutach jest liczbą nieparzystą i większą od 9.

Zadanie 6

Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia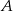
– na każdej kostce wypadła nieparzysta liczba oczek,
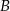– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 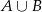A ∪ B .

Zadanie 7

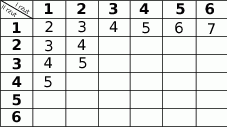
Gracz rzuca dwa razy symetryczną sześcienną kostką do gry i oblicza sumę wyrzuconych oczek. Jeśli suma ta jest jedną z liczb: 6, 7 lub 8, to gracz wygrywa. W pozostałych przypadkach przegrywa.

Uzupełnij tabelę, tak aby przedstawiała wszystkie możliwe wyniki tego doświadczenia losowego.
Podaj liczbę wyników sprzyjających wygranej gracza i oblicz prawdopodobieństwo wygranej.

Zadanie 8

Rzucamy dwiema sześciennymi kostkami.

Jakie jest prawdopodobieństwo, że suma oczek będzie równa 4?
Czy bardziej prawdopodobne jest, że suma wyrzuconych oczek będzie równa 5, czy że będzie równa 10?
Jakie jest najbardziej prawdopodobna suma wyrzuconych oczek?

Zadanie 9

Rzucamy dwukrotnie kostką, które ze zdarzeń jest bardziej prawdopodobne:
– w pierwszym rzucie otrzymamy liczbę oczek mniejszą niż w drugim;
– suma oczek, jakie wypadną w obydwu rzutach, jest nie mniejsza od 8?

Zadanie 10

Rzucamy dwiema sześciennymi kostkami.

Jakie jest prawdopodobieństwo, że różnica między liczbami oczek wyrzuconych na kostkach (od większej odejmujemy mniejszą) będzie równa 2?
Jaka jest najbardziej prawdopodobna różnica między wynikami na kostkach (od większego odejmujemy mniejszy)?

Zadanie 11

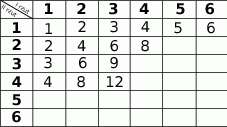
Gracz rzuca dwa razy symetryczną sześcienną kostką do gry i oblicza iloczyn wyrzucanych oczek. Jeśli iloczyn ten jest liczbą podzielną przez 2 lub przez 3 to przegrywa. W pozostałych przypadkach wygrywa.

Uzupełnij tabelkę tak, aby przedstawiała wszystkie wyniki tego doświadczenia.
Podaj liczbę wynikow sprzyjających wygranej gracza i oblicz prawdopodobieństwo wygranej.

Zadanie 12

Ze zbioru liczb 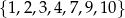{1,2,3,4 ,7 ,9,10} losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.

Zadanie 13

Paulina ma w szaﬁe 20 bluzek w kilku kolorach. W tabelce przedstawiono, jaki procent bluzek stanowią bluzki w danym kolorach

Kolor bluzki	%
czerwony	15
niebieski	70
czarny	5
biały	10

Oblicz prawdopodobieństwo, że wybrana losowo bluzka jest niebieska.

Zadanie 14

Poniższy diagram przedstawia wyniki ankiety znajomości języków obcych wśród uczniów pewnej szkoły.

Oblicz prawdopodobieństwo, że losowo wybrana osoba z ankietowanych zna

język angielski,
co najmniej jeden język obcy.

Zadanie 15

Każdej karcie bankomatowej jest przypisany numer identyﬁkacyjny zwany kodem PIN. Kod ten składa się z czterech cyfr (cyfry mogą się powtarzać, ale kodem PIN nie może być 0000). Oblicz prawdopodobieństwo, że w losowo utworzonym kodzie PIN żadna cyfra się nie powtórzy. Wynik podaj w postaci ułamka nieskracalnego.

Zadanie 16

Oblicz prawdopodobieństwo wylosowania spośród wszystkich liczb trzycyfrowych liczby, której suma cyfr jest równa 2?

Zadanie 17

Spośród cyfr 1, 2, 3, 4, 5, 6 losujemy kolejno dwa razy po jednej cyfrze ze zwracaniem. Tworzymy liczbę dwucyfrową w ten sposób, że pierwsza z wylosowanych cyfr jest cyfrą dziesiątek, a druga cyfrą jedności tej liczby. Oblicz prawdopodobieństwo utworzenia liczby większej od 52.

Zadanie 18

Przeprowadzono badania, dotyczące liczby osób jadących w samochodach osobowych w godzinach rannych, w kierunku centrum pewnego miasta. Wyniki badań przedstawione są na digramie kołowym.

Oblicz średnią liczbę osób jadących w samochodzie osobowym w godzinach rannych w kierunku centrum.
Oblicz prawdopodobieństwo, że w losowo wybranym samochodzie osobowym, w godzinach rannych, w kierunku centrum, były więcej niż 3 osoby.
Wiedząc, że samochodów osobowych, w których były 4 osoby, zaobserwowano o 350 więcej, niż samochodów w których było 5 osób, oblicz, ile wszystkich samochodów obserwowano w trakcie badań.

Zadanie 19

Przedstawiono informacje dotyczące znajomości języka angielskiego oraz języka niemieckiego w pewnej 200 osobowej grupie studentów:
25% studentów zna język angielski i język niemiecki,
50% studentów zna język niemiecki,
60% zna język angielski.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany z tej grupy student

zna język angielski i nie zna języka niemieckiego,
nie zna języka angielskiego i nie zna języka niemieckiego.

Zadanie 20

Z talii 52 kart wyciągamy losowo jedną. Oblicz prawdopodobieństwo, że wyciągnięta karta będzie damą lub treﬂem.

Zadanie 21

Z talii 52 kart losujemy jedną kartę.

Oblicz prawdopodobieństwo zdarzeń:
A – losowo wybrana karta jest pikiem.
B – losowo wybrana karta jest asem.
Oblicz prawdopodobieństwo zdarzeń 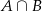oraz .

Zadanie 22

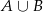Losujemy jedną z 52 kart. Jakie jest prawdopodobieństwo wyciągnięcia asa lub króla?

Zadanie 23

Z talii 52 kart losujemy bez zwracania dwie karty. Jakie jest prawdopodobieństwo wylosowania dwóch asów?

Zadanie 24

O zdarzeniach losowych 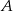i 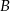wiemy, że: 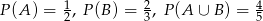1 2 4 P(A ) = 2 , P (B) = 3, P (A ∪ B) = 5 . Oblicz:

Zadanie 25

Dla zdarzeń 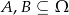A ,B ⊆ Ω spełnione są warunki 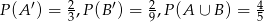′ 2 ′ 2 4 P (A ) = 3,P (B ) = 9 ,P (A ∪ B ) = 5 . Oblicz P (A ∩ B ) .

Zadanie 26

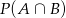Wiadomo, że 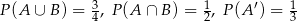3 1 ′ 1 P (A ∪ B ) = 4, P(A ∩ B ) = 2, P(A ) = 3 . Oblicz prawdopodobieństwa zdarzeń 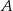i .

Zadanie 27

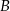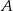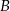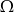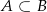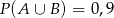Zdarzenia losowe i są zawarte w przestrzeni . Wiedząc, że A ⊂ B oraz P (A ∪ B ) = 0,9 , oblicz P(B ′) .

Zadanie 28

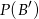W garderobie pani Joanny wiszą 3 żakiety: biały, zielony i granatowy oraz 4 spódnice: czarna, biała, granatowa i szara. Oblicz prawdopodobieństwo zdarzenia, że wybierając losowo jeden żakiet i jedną spódnicę, pani Joanna skompletuje strój w jednym kolorze.

Zadanie 29

W koszu znajdują się owoce: 12 jabłek i 8 pomarańczy. Wyjmujemy kolejno trzy owoce, nie odkładając ich do kosza. Jakie jest prawdopodobieństwo, że wylosujemy dokładnie dwie pomarańcze.

Zadanie 30

W każdym z dwóch koszyków znajduje się 5 klocków czerwonych, 10 zielonych i 6 białych. Wyjmujemy losowo po jednym klocku z każdego koszyka. Oblicz prawdopodobieństwo, że:

wylosujemy dwa klocki białe;
wylosujemy klocki tego samego koloru.

Zadanie 31

Losujemy jedną kartę spośród wszystkich króli z talii oraz jedną kartę spośród wszystkich dam. Jakie jest prawdopodobieństwo otrzymania w ten sposób dwóch kart tego samego koloru np. dwóch treﬂii lub dwóch kar?

Zadanie 32

W jednej urnie są 3 kule: czerwona, biała i zielona, a w drugiej urnie są 2 kule: czerwona i biała. Losujemy po jednej kuli z każdej urny. Jakie jest prawdopodobieństwo wyciągnięcia dwóch kul w tym samym kolorze?

Zadanie 33

W jednej szuﬂadzie znajduje się 6 czapek: 3 zielone, 2 czerwone i 1 niebieska, a w drugiej szuﬂadzie jest 7 szalików: 2 zielone, 1 czerwony i 4 niebieskie. Wyjęto losowo jedną czapkę i jeden szalik. Oblicz prawdopodobieństwo zdarzenia A – wylosowana czapka i wylosowany szalik są tego samego koloru.

Zadanie 34

Dane są dwa pojemniki. W pierwszym z nich znajduje się 9 kul: 4 białe, 3 czarne i 2 zielone. W drugim pojemniku jest 6 kul: 2 białe , 3 czarne i 1 zielona. Z każdego pojemnika losujemy po jednej kuli. Oblicz prawdopodobieństwo wylosowania dwóch kul tego samego koloru.

Zadanie 35

W dwóch pudełkach są cukierki. W pierwszym pudełku jest 15 cukierków czekoladowych i 5 owocowych, a w drugim pudełku jest 20 cukierków czekoladowych i 30 cukierków owocowych. Losujemy cukierek najpierw z pierwszego, a potem z drugiego pudełka. Jakie jest prawdopodobieństwo, że w wyniku losowania otrzymamy dwa cukierki czekoladowe?

Arkusz Wersja PDF