Zestaw użytkownika nr 3337_4828
Zestaw użytkownika
nr 3337_4828
Rozwiąż nierówność 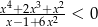 .
.
Określ liczbę pierwiastków równania 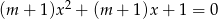 w zależności od wartości parametru
w zależności od wartości parametru 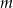 , a następnie naszkicuj wykres funkcji:
, a następnie naszkicuj wykres funkcji:

Dziedziną funkcji 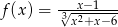 jest zbiór
jest zbiór
A) 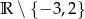 B)
B) 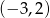 C)
C) 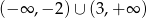 D)
D) 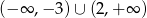
Rozwiązaniem równania 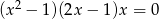 nie jest liczba
nie jest liczba
A) 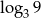 B)
B) 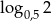 C)
C) 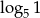 D)
D) 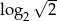
Dany jest ciąg arytmetyczny 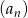 dla
dla 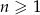 , w którym
, w którym 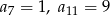 .
.
- Oblicz pierwszy wyraz
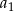 i różnicę
i różnicę  ciągu
ciągu 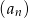 .
. - Sprawdź, czy ciąg
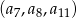 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 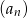 miała wartość najmniejszą.
miała wartość najmniejszą.
Rozwiąż równanie 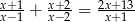 .
.
Rozwiązaniem równania 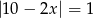 są liczby
są liczby
A) całkowite B) różniące się o 1 C) niewymierne D) przeciwne
Dla jakich wartości parametru 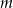 równanie
równanie 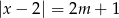 ma jedno rozwiązanie?
ma jedno rozwiązanie?
Odwrotność liczby będącej rozwiązaniem równania 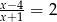 jest równa
jest równa
A) 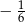 B)
B) 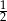 C) 6 D)
C) 6 D) 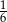
Rozwiąż równanie 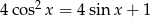 w przedziale
w przedziale 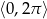 .
.
Wskaż nierówność, którą spełnia liczba 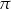 .
.
A) 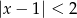 B)
B) 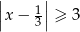 C)
C) 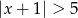 D)
D) 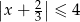
Rozwiąż układ równań:
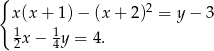
Jeżeli 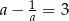 to liczba
to liczba 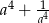 jest równa
jest równa
A) 121 B) 123 C) 81 D) 119
Wiedząc, że liczba 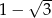 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 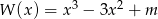 , wyznacz wartość parametru
, wyznacz wartość parametru 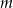 .
.
Wyznacz wszystkie rozwiązania równania 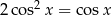 należące do przedziału
należące do przedziału 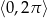 .
.
Wyrażenie 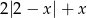 dla
dla 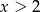 ma wartość
ma wartość
A) 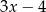 B) 5 C)
B) 5 C) 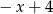 D) 1
D) 1
Rozwiąż nierówność
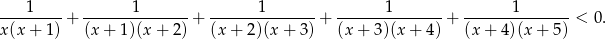
Rozwiąż równanie 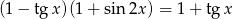 .
.
Dla jakich wartości parametru 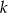 rozwiązanie układu równań
rozwiązanie układu równań 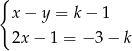 spełnia warunek
spełnia warunek 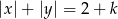 ?
?
Rozwiąż nierówność 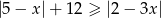 .
.
Rozwiąż równanie 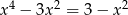 .
.
Rozwiąż równanie 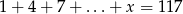 .
.

