Zestaw użytkownika nr 3413_4598
Egzamin poprawkowy z matematyki27 Sierpnia 2012Czas pracy: 45 min.Suma punktów: 25
Stopień wielomianu 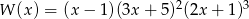 jest równy
jest równy
A) 8 B) 6 C) 4 D) 5
Dane są wielomiany 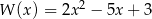 i
i 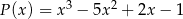 . Wielomian
. Wielomian 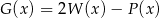 jest równy
jest równy
A) 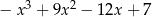 B)
B) 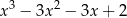 C)
C) 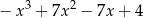 D)
D) 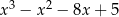
Liczba 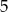 nie należy do dziedziny wyrażenia
nie należy do dziedziny wyrażenia
A) 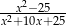 B)
B) 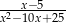 C)
C) 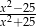 D)
D) 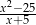
Przedstawiony na rysunku wykres może być wykresem funkcji
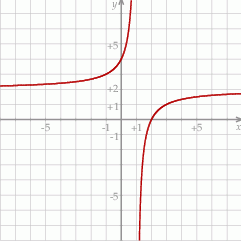
A) 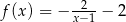 B)
B) 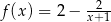 C)
C) 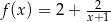 D)
D) 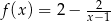
Pole powierzchni całkowitej sześcianu jest równe 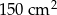 . Długość przekątnej podstawy tego sześcianu jest równa
. Długość przekątnej podstawy tego sześcianu jest równa
A) 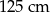 B)
B) 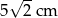 C)
C) 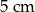 D)
D) 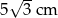
Ostrosłup ma 18 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 27 B) 11 C) 34 D) 18
W barze są do wyboru: 4 zupy, 5 drugich dań i 3 desery. Ile różnych dań obiadowych złożonych z zupy, drugiego dania i deseru można zamówić w tym barze? (Za różne uważamy zestawy, które różnią się przynajmniej jednym elementem).
Oblicz, ile jest liczb naturalnych czterocyfrowych, w których zapisie pierwsza cyfra jest parzysta, a pozostałe nieparzyste.
Rozwiąż równanie 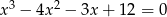 .
.
Rozwiąż równanie 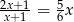 .
.
W jednej urnie są 3 kule: czerwona, biała i zielona, a w drugiej urnie są 2 kule: czerwona i biała. Losujemy po jednej kuli z każdej urny. Jakie jest prawdopodobieństwo wyciągnięcia dwóch kul w tym samym kolorze?
Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że suma oczek będzie równa 4?
Podstawą prostopadłościanu jest kwadrat. Przekątna tego prostopadłościanu ma długość 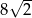 i jest nachylona do płaszczyzny podstawy pod kątem
i jest nachylona do płaszczyzny podstawy pod kątem 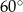 . Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek.
. Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek.
Oblicz objętość kuli wiedząc że jej pole powierzchni jest równe 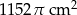 .
.
Stożek ma wysokość 10 cm. Pole przekroju osiowego tego stożka jest równe 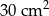 . Jaką długość ma tworząca tego stożka?
. Jaką długość ma tworząca tego stożka?

