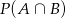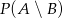Zestaw użytkownika nr 3438_4133
Zestaw użytkownika
nr 3438_4133
Ze zbioru cyfr 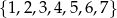 losujemy kolejno bez zwracania dwie cyfry i zapisujemy je, tworząc liczbę dwucyfrową. Ile jest możliwości utworzenia w ten sposób liczby podzielnej przez 3?
losujemy kolejno bez zwracania dwie cyfry i zapisujemy je, tworząc liczbę dwucyfrową. Ile jest możliwości utworzenia w ten sposób liczby podzielnej przez 3?
A) 6 B) 12 C) 15 D) 14
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia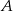 – na każdej kostce wypadła nieparzysta liczba oczek,
– na każdej kostce wypadła nieparzysta liczba oczek,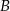 – suma wyrzuconych oczek jest nie mniejsza niż 8.
– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 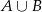 .
.
Ze zbioru liczb 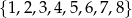 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 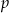 jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
A) 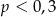 B)
B) 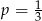 C)
C) 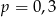 D)
D) 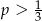
Z urny, w której jest 6 kul czarnych i 4 żółte, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule jednakowych kolorów.
W pudełku zmieszano 30 ziaren fasoli, 20 ziaren ciecierzycy i 50 ziaren grochu.
- Losujemy jedno ziarenko. Jakie jest prawdopodobieństwo wylosowania ziarenka ciecierzycy?
- Jako pierwsze wylosowano ziarenko fasoli. Jakie jest prawdopodobieństwo, że drugim wylosowanym ziarenkiem nie będzie ziarenko fasoli?
- Z pudełka usunięto po 10% ziarenek każdego rodzaju. Jakie jest prawdopodobieństwo wylosowania ziarenka fasoli?
Dane są zbiory liczb całkowitych: 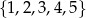 i
i 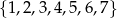 . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
. Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
Spośród 5 monet jednozłotowych, 7 dwuzłotowych i 6 pięciozłotowych wybieramy 3 monety. Oblicz prawdopodobieństwo, że wszystkie trzy monety będą miały ten sam nominał.
W koszu znajdują się owoce: 12 jabłek i 8 pomarańczy. Wyjmujemy kolejno trzy owoce, nie odkładając ich do kosza. Jakie jest prawdopodobieństwo, że wylosujemy dokładnie dwie pomarańcze.
Z pojemnika, w którym są dwa losy wygrywające i trzy losy puste, losujemy dwa razy po jednym losie bez zwracania. Oblicz prawdopodobieństwo, że otrzymamy co najmniej jeden los wygrywający. Wynik przedstaw w postaci ułamka nieskracalnego.
Na loterii jest 10 losów, z których 4 są wygrywające. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A)  B)
B) 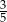 C)
C)  D)
D) 
O zdarzeniach losowych 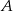 i
i 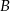 wiemy, że:
wiemy, że: 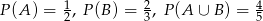 . Oblicz:
. Oblicz:
Ze zbioru 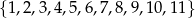 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 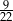 B)
B) 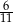 C)
C) 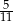 D)
D) 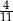
Ze zbioru liczb 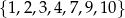 losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.
losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.
Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 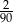 B)
B) 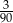 C)
C) 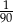 D)
D) 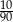
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia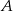 – na każdej kostce wypadła nieparzysta liczba oczek,
– na każdej kostce wypadła nieparzysta liczba oczek,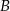 – suma wyrzuconych oczek jest nie mniejsza niż 8.
– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 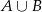 .
.