Zestaw użytkownika nr 3472_6374
Zestaw użytkownika
nr 3472_6374
Wykaż, że prosta 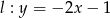 jest styczna do okręgu
jest styczna do okręgu 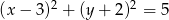 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 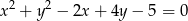 .
.
Wyznacz współrzędne punktów wspólnych prostej 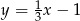 i okręgu
i okręgu 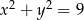 .
.
Wyznacz równanie okręgu o środku 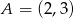 , stycznego do prostej o równaniu
, stycznego do prostej o równaniu 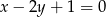 .
.
Ile punktów wspólnych ma okrąg o równaniu 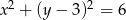 z prostą o równaniu
z prostą o równaniu 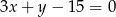 ?
?
Określ wzajemne położenie prostej 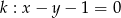 i okręgu o równaniu
i okręgu o równaniu 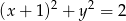 .
.
Wyznacz odległość punktu 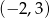 od prostej o równaniu
od prostej o równaniu 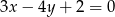 .
.
W układzie współrzędnych dane są dwa punkty: 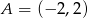 i
i 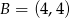 .
.
- Wyznacz równanie symetralnej odcinka
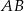 .
. - Prosta
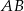 oraz prosta o równaniu
oraz prosta o równaniu 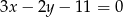 przecinają się w punkcie
przecinają się w punkcie 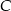 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 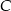 .
.
Określ wzajemne położenie prostych 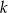 i
i 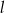 o równaniach
o równaniach
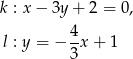
Dany jest punkt 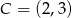 i prosta o równaniu
i prosta o równaniu 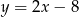 będąca symetralną odcinka
będąca symetralną odcinka 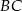 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 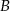 . Wykonaj obliczenia uzasadniające odpowiedź.
. Wykonaj obliczenia uzasadniające odpowiedź.
Wyznacz równanie prostej równoległej do prostej 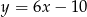 przechodzącej przez punkt
przechodzącej przez punkt 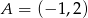 oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt
oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt 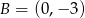 .
.
Zapisz równanie ogólne i kierunkowe prostej 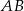 , jeśli
, jeśli 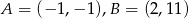 .
.
Określ wzajemne położenie prostych 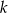 i
i 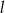 o równaniach
o równaniach
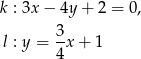
Proste o równaniach 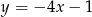 i
i 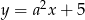 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Wyznacz punkt wspólny symetralnej odcinka 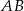 , gdzie
, gdzie 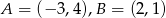 , oraz osi
, oraz osi 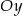 .
.
Punkt 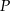 jest punktem wspólnym przekątnych trapezu
jest punktem wspólnym przekątnych trapezu 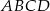 , w którym
, w którym 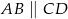 oraz
oraz ![−→ −→ −→ D = (1 0,− 9),AB = [12,21],CB = [0,13],CP = [− 3,− 2]](https://img.zadania.info/zad/6347587/HzadT3x.gif) . Oblicz współrzędne pozostałych wierzchołków trapezu
. Oblicz współrzędne pozostałych wierzchołków trapezu 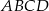 .
.
Oblicz odległość punktu 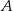 od środka odcinka
od środka odcinka 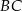 , gdzie
, gdzie 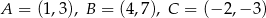 .
.
Punkt 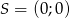 jest środkiem boku
jest środkiem boku 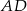 równoległoboku
równoległoboku 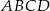 . Wiadomo też, że
. Wiadomo też, że ![−→ AB = [4;3]](https://img.zadania.info/zad/9290117/HzadT3x.gif) oraz
oraz ![−→ BC = [6;2]](https://img.zadania.info/zad/9290117/HzadT4x.gif) . Wyznacz wierzchołki tego równoległoboku.
. Wyznacz wierzchołki tego równoległoboku.
W układzie współrzędnych na płaszczyźnie punkty 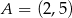 i
i 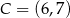 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 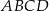 . Wyznacz równanie prostej
. Wyznacz równanie prostej 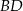 .
.
Dany jest równoległobok 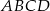 o wierzchołkach
o wierzchołkach 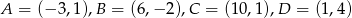 . Napisz równania prostych, w których zawarte są przekątne równoległoboku.
. Napisz równania prostych, w których zawarte są przekątne równoległoboku.
W kwadracie 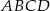 dane są wierzchołek
dane są wierzchołek 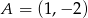 i środek symetrii
i środek symetrii 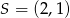 . Oblicz pole kwadratu
. Oblicz pole kwadratu  .
.
Dane są punkty 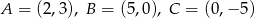 .
.
- Uzasadnij, że proste
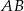 i
i 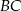 są prostopadłe.
są prostopadłe. - Wyznacz współrzędne takiego punktu
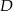 , dla którego czworokąt
, dla którego czworokąt 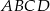 jest prostokątem.
jest prostokątem. - Oblicz pole prostokąta
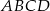 .
.
Wyznacz równanie okręgu wpisanego w kwadrat 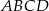 , gdzie
, gdzie 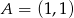 i
i 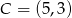 .
.
Wyznacz równanie okręgu opisanego na prostokącie 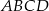 , w którym
, w którym 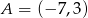 i
i 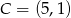 .
.
W okrąg o równaniu 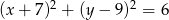 wpisano kwadrat. Oblicz pole tego kwadratu.
wpisano kwadrat. Oblicz pole tego kwadratu.

