Zestaw użytkownika nr 3509_6336
Zestaw użytkownika
nr 3509_6336
Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu 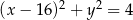 jest okrąg o równaniu
jest okrąg o równaniu 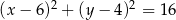 , a skala tej jednokładności jest liczbą ujemną.
, a skala tej jednokładności jest liczbą ujemną.
Przekształcenie 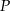 określone jest w następujący sposób:
określone jest w następujący sposób: 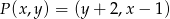 , gdzie
, gdzie 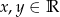 .
.
- Wykaż, że przekształcenie
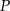 jest izometrią.
jest izometrią. - W prostokątnym układzie współrzędnych narysuj trójkąt o wierzchołkach
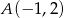 ,
, 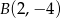 ,
, 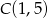 , a następnie znajdź jego obraz w przekształceniu
, a następnie znajdź jego obraz w przekształceniu 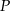 .
. - Wyznacz równanie prostej zawierającej wysokość trójkąta
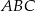 poprowadzoną na bok
poprowadzoną na bok 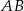 .
. - Oblicz pole trójkąta
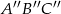 , który jest obrazem trójkąta
, który jest obrazem trójkąta 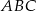 w jednokładności o środku w punkcie (0,0) i skali
w jednokładności o środku w punkcie (0,0) i skali 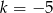 .
.
Dane są punkty 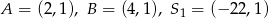 i
i 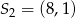 . Odcinek
. Odcinek 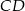 jest obrazem odcinka
jest obrazem odcinka 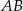 w jednokładności o skali dodatniej i środku
w jednokładności o skali dodatniej i środku 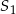 , jak i w jednokładności o skali ujemnej i środku
, jak i w jednokładności o skali ujemnej i środku 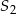 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 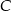 i
i 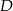 .
.
Końcami odcinka są punkty o współrzędnych 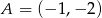 oraz
oraz 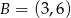 . Odcinek
. Odcinek 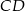 jest obrazem odcinka
jest obrazem odcinka 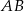 zarówno w jednokładności o dodatniej skali i środku
zarówno w jednokładności o dodatniej skali i środku 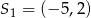 , jak i w jednokładności o ujemnej skali i środku
, jak i w jednokładności o ujemnej skali i środku 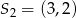 . Oblicz współrzędne końców odcinka
. Oblicz współrzędne końców odcinka 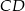 oraz skalę jednokładności o środku
oraz skalę jednokładności o środku 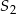 .
.
Kwadrat o wierzchołkach 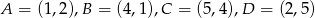 przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach
przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach 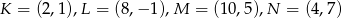 . Wyznacz środek i skalę tej jednokładności.
. Wyznacz środek i skalę tej jednokładności.
Odcinek 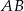 , gdzie
, gdzie 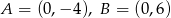 , jest przeciwprostokątną trójkąta prostokątnego
, jest przeciwprostokątną trójkąta prostokątnego 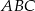 . Wierzchołek
. Wierzchołek 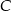 o ujemnej odciętej należy do prostej
o ujemnej odciętej należy do prostej 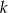 o równaniu
o równaniu 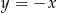 .
.
- Oblicz współrzędne wierzchołka
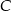 .
. - Obrazem trójkąta
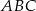 w jednokładności o środku
w jednokładności o środku 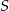 i skali
i skali 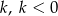 , jest trójkąt
, jest trójkąt 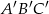 , którego pole wynosi 5. Wiedząc dodatkowo, że
, którego pole wynosi 5. Wiedząc dodatkowo, że 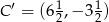 , oblicz skalę jednokładności i współrzędne punktu
, oblicz skalę jednokładności i współrzędne punktu 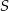 .
.
W jednokładności o środku 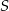 i skali
i skali 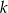 obrazem okręgu o równaniu
obrazem okręgu o równaniu 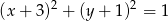 jest okrąg o równaniu
jest okrąg o równaniu 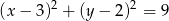 . Oblicz współrzędne środka
. Oblicz współrzędne środka 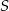 jednokładności.
jednokładności.
Dany jest okrąg 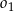 o równaniu
o równaniu 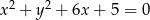 oraz okrąg
oraz okrąg 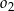 o równaniu
o równaniu 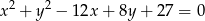 . Oblicz współrzędne środka jednokładności i skalę jednokładności, w której obrazem okręgu
. Oblicz współrzędne środka jednokładności i skalę jednokładności, w której obrazem okręgu 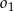 jest okrąg
jest okrąg 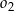 .
.
Wyznacz równanie okręgu, który jest obrazem okręgu 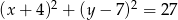 w jednokładności o środku
w jednokładności o środku 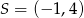 i skali
i skali 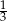 .
.

