Zestaw użytkownika nr 3532_5736
Zestaw użytkownika
nr 3532_5736
Reszta z dzielenia wielomianu 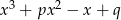 przez trójmian
przez trójmian 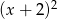 wynosi
wynosi 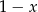 . Wyznacz pierwiastki tego wielomianu.
. Wyznacz pierwiastki tego wielomianu.
Wielomian 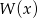 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 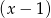 ,
, 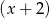 ,
, 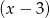 daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian
daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 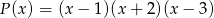 .
.
Reszta z dzielenia wielomianu 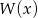 przez wielomian
przez wielomian 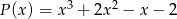 jest równa
jest równa 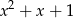 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 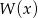 przez wielomian
przez wielomian 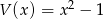 .
.
Liczba 2 jest miejscem zerowym wielomianu 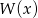 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 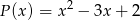 jeśli wiadomo, że w wyniku dzielenia wielomianu
jeśli wiadomo, że w wyniku dzielenia wielomianu 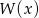 przez dwumian
przez dwumian 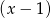 otrzymujemy resztę 5.
otrzymujemy resztę 5.
Reszta z dzielenia wielomianu 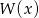 przez dwumian
przez dwumian 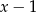 jest równa 1, zaś reszta z dzielenia tego wielomianu przez
jest równa 1, zaś reszta z dzielenia tego wielomianu przez 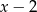 jest równa 4. Wyznacz resztę z dzielenia wielomianu
jest równa 4. Wyznacz resztę z dzielenia wielomianu 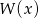 przez wielomian
przez wielomian 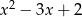 .
.
Dany jest wielomian 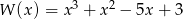 .
.
- Oblicz resztę z dzielenia tego wielomianu przez dwumian
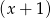 .
. - Oblicz miejsca zerowe tego wielomianu.
- Rozwiąż nierówność
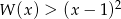 .
.
Nie wykonując dzielenia, wyznacz resztę z dzielenia wielomianu 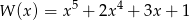 przez
przez 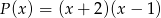 .
.
Dana jest funkcja 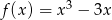 dla
dla 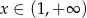 . Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale
. Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale 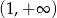 .
.
Wielomian 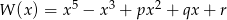 jest podzielny przez wielomian
jest podzielny przez wielomian 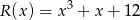 . Wyznacz liczby
. Wyznacz liczby 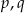 i
i  .
.
Dane są wielomiany 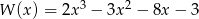 i
i 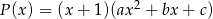 .
.
- Wyznacz współczynniki
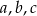 tak, aby
tak, aby 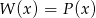 .
. - Przedstaw wielomian
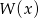 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych.
Dla jakich wartości parametru 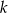 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 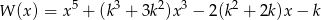 przez dwumian
przez dwumian 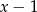 jest nie większa od (–2)?
jest nie większa od (–2)?
Dla jakich wartości parametru  , wielomian
, wielomian 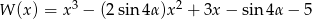 jest podzielny przez dwumian
jest podzielny przez dwumian 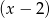 ?
?

