Zestaw użytkownika nr 3539_5256
Zestaw użytkownika
nr 3539_5256
Łódź musi płynąć 60km w dół rzeki, a następnie 10km w górę rzeki. Prędkość prądu rzeki wynosi 5km/godz. Jaka powinna być prędkość własna łodzi, aby cała podróż nie trwała dłużej niż 10 godzin?
Rowerzysta w ciągu pierwszej godziny przejechał 21 km, a w ciągu każdej następnej godziny – odcinek o 0,75 km krótszy od poprzedniego. Jaką drogę pokonał rowerzysta i w jakim czasie, jeśli w ciągu ostatniej godziny przejechał 18 km?
Z dwóch miast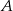 
i 
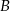, odległych od siebie o 18 kilometrów, wyruszyli naprzeciw siebie dwaj turyści. Pierwszy turysta wyszedł z miasta 
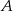o jedną godzinę wcześniej niż drugi z miasta 
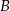. Oblicz prędkość, z jaką szedł każdy turysta, jeżeli wiadomo, że po spotkaniu pierwszy turysta szedł do miasta 
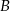jeszcze 1,5 godziny, drugi zaś szedł jeszcze 4 godziny do miasta 
.
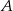Po torze wodnym o długości 10 km pływają w kółko dwie łodzie motorowe, przy czym druga z nich płynie z prędkością o 5 km/h większą od prędkości pierwszej łodzi. Łodzie te wystartowały z tego samego punktu i ponownie spotkały się, gdy pierwsza z łodzi wykonała pełne 3 okrążenia toru. Oblicz średnie prędkości obu łodzi.
Rowerzysta jedzie ze stałą prędkością 20km/h.
- Napisz wzór wyrażający drogę
rowerzysty w ciągu 
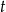godzin. - Sporządź tabelkę wartości
dla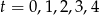 
. - Naszkicuj wykres zależności
od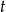 
.
Kuba pożyczył od taty samochód, którym wyruszył z domu na spotkanie ze swoją dziewczyną. Przed wyjazdem obliczył, że jadąc ze średnią prędkościa 60km/h przybędzie na spotkanie dokładnie o umówionej godzinie. Po przejechaniu (z zaplanowaną prędkością) 60% drogi "złapał gumę", a zmiana koła zajęła mu 16 minut. Teraz, aby zdążyć na spotkanie, musiałby jechać z prędkością 120km/h. Oblicz odległość od domu Kuby do miejsca spotkania z ukochaną.
Samochód jadący autostradą pali 5,6 litra paliwa na 100km. Napisz wzór funkcji 
określającej przebytą drogę (w kilometrach) w zależnosci od zużytego paliwa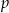 
(w litrach).
