Definicje Wielomianem nazywamy wyrażenie (funkcję) postaci
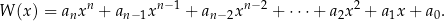
Jeżeli 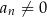 to mówimy, że
to mówimy, że 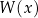 jest wielomianem stopnia
jest wielomianem stopnia  . Stopień wielomianu zwykle oznacza się jednym z symboli (od ang. degree)
. Stopień wielomianu zwykle oznacza się jednym z symboli (od ang. degree)
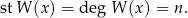
W myśl powyższej definicji funkcje kwadratoweto wielomiany stopnia 2, funkcje liniowe to wielomiany stopnia 1, niezerowe funkcje stałe to wielomiany stopnia 0.
Zwyczajowowielomiany liniowe 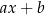 nazywamy dwumianami (mają dwa składniki), a wielomiany kwadratowe
nazywamy dwumianami (mają dwa składniki), a wielomiany kwadratowe 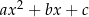 trójmianami. Nie należy tej terminologii traktować zbyt dosłownie, np. wielomian
trójmianami. Nie należy tej terminologii traktować zbyt dosłownie, np. wielomian 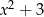 nadal uważamy za trójmian, chociaż ma tylko dwa składniki.
nadal uważamy za trójmian, chociaż ma tylko dwa składniki.
Liczby 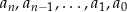 nazywamy współczynnikami wielomianu
nazywamy współczynnikami wielomianu 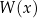 . Współczynnik
. Współczynnik 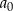 zwykle nazywa się wyrazem wolnym wielomianu
zwykle nazywa się wyrazem wolnym wielomianu 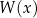 (jest wolny od zmiennej).
(jest wolny od zmiennej).
Mówimy, że dwa wielomiany są równe jeżeli mają identyczne współczynniki. Tak się szczęśliwie składa, że równość dwóch wielomianów (czyli równość ich współczynników) to dokładnie to samo co równość wyznaczonych przez nie funkcji. Z własności tej często korzysta się w zadaniach szkolnych.
Wyznaczmy wartości parametrów  i
i 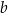 , dla których równanie
, dla których równanie
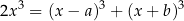
jest spełnione przez każdą liczbę rzeczywistą.
Korzystając ze wzorów skróconego mnożenia możemy przekształcić równanie do postaci:
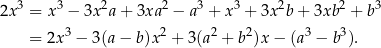
Skoro te dwa wielomiany mają być równe, to muszą mieć równe współczynniki. W szczególności 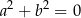 , czyli
, czyli 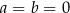 .
.
Wykresy Znajomość kształtów wykresów wielomianów jest niezbędna do sprawnego rozwiązywania zadań, dlatego warto poświęcić chwilę na ich naukę. Jest kilka prostych zasad, które pozwalają niemal automatycznie naszkicować wykres wielomianu.
O wartościach wielomianu w 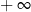 i
i 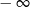 (czyli jak się zachowuje wykres gdy jedziemy z
(czyli jak się zachowuje wykres gdy jedziemy z  do
do 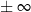 ) decyduje tylko i wyłącznie składnik
) decyduje tylko i wyłącznie składnik 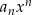 , a więc praktycznie
, a więc praktycznie 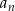 (tak jest, bo dla bardzo dużych/bardzo małych liczb, wartość
(tak jest, bo dla bardzo dużych/bardzo małych liczb, wartość 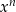 jest o wiele większa/mniejsza niż wartości pozostałych składników).
jest o wiele większa/mniejsza niż wartości pozostałych składników).
Jakie są zatem możliwe konfiguracje? Jeżeli 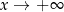 , to wyrażenie
, to wyrażenie 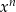 też dąży do nieskończoności, a więc zachowanie
też dąży do nieskończoności, a więc zachowanie 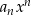 zależy tylko od znaku
zależy tylko od znaku 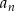 : jeżeli
: jeżeli 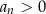 to
to 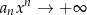 , a jeżeli
, a jeżeli 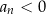 to
to 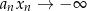 .
.
Odrobinę ciekawsza jest sytuacja w 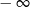 , bo wartość wyrażenia
, bo wartość wyrażenia 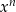 może być dodatnia gdy
może być dodatnia gdy  jest parzyste i ujemna, gdy
jest parzyste i ujemna, gdy  jest nieparzyste. Do tego dochodzi znak
jest nieparzyste. Do tego dochodzi znak 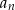 : jeżeli jest ujemny, to wyrażenia
: jeżeli jest ujemny, to wyrażenia 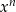 i
i 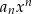 mają przeciwne znaki. W sumie mamy 4 możliwości, które są szkicowo przedstawione na poniższym rysunku.
mają przeciwne znaki. W sumie mamy 4 możliwości, które są szkicowo przedstawione na poniższym rysunku.
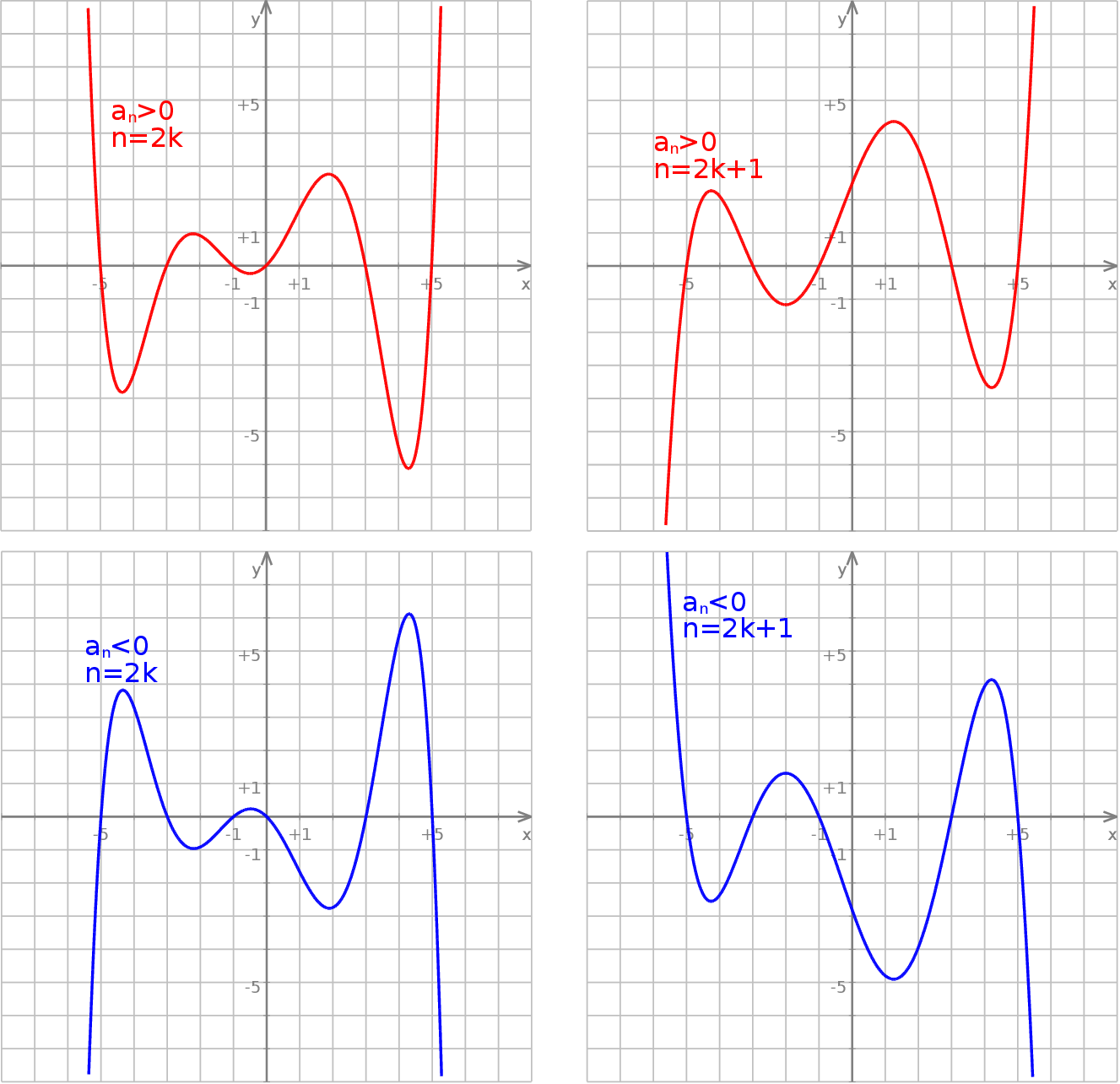
Jak to zapamiętać? Przede wszystkim trzeba pamiętać, że patrzymy tylko na wyraz z najwyższą potęgą  . A potem wystarczy już trochę zdrowego rozsądku: myślimy sobie jaka jest wartość wyrażenia
. A potem wystarczy już trochę zdrowego rozsądku: myślimy sobie jaka jest wartość wyrażenia 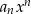 , gdy wstawiamy do niego bardzo duże liczby, i gdy wstawiamy bardzo małe (ujemne!) liczby. Jeżeli nauczymy się tak myśleć, to od razu będziemy wiedzieli, gdzie są końce interesującego nas wykresu.
, gdy wstawiamy do niego bardzo duże liczby, i gdy wstawiamy bardzo małe (ujemne!) liczby. Jeżeli nauczymy się tak myśleć, to od razu będziemy wiedzieli, gdzie są końce interesującego nas wykresu.
Inny sposób, to nauczyć się, że dla 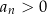 wykres zawsze zaczyna się w prawym górnym rogu, a z lewej strony wychodzi górnym rogiem, jeżeli
wykres zawsze zaczyna się w prawym górnym rogu, a z lewej strony wychodzi górnym rogiem, jeżeli  jest parzyste i dolnym jeżeli
jest parzyste i dolnym jeżeli  jest nieparzyste. Wykresy dla
jest nieparzyste. Wykresy dla 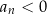 otrzymujemy odbijając wykresy z
otrzymujemy odbijając wykresy z 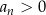 względem osi
względem osi 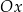 .
.
No to wiemy gdzie są końce wykresu, a co jest w środku? Tu już nie ma tak prostej odpowiedzi, ale jedna prosta reguła, to że górek/dołków jest w sumie co najwyżej 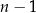 (na ogół jest dokładnie
(na ogół jest dokładnie 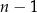 , ale może być mniej). Oczywiście na przemian mamy górki i dołki. W większości zastosowań taka ogólna wiedza o kształcie wykresu jest w zupełności wystarczająca.
, ale może być mniej). Oczywiście na przemian mamy górki i dołki. W większości zastosowań taka ogólna wiedza o kształcie wykresu jest w zupełności wystarczająca.
Na lewym wykresie mamy typowy wykres wielomianu stopnia 3 z dodatnim współczynnikiem przy 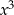 : biegnie on od lewego dolnego rogu do prawego górnego, po drodze jest jedna górka i jeden dołek (w sumie
: biegnie on od lewego dolnego rogu do prawego górnego, po drodze jest jedna górka i jeden dołek (w sumie 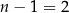 ).
).
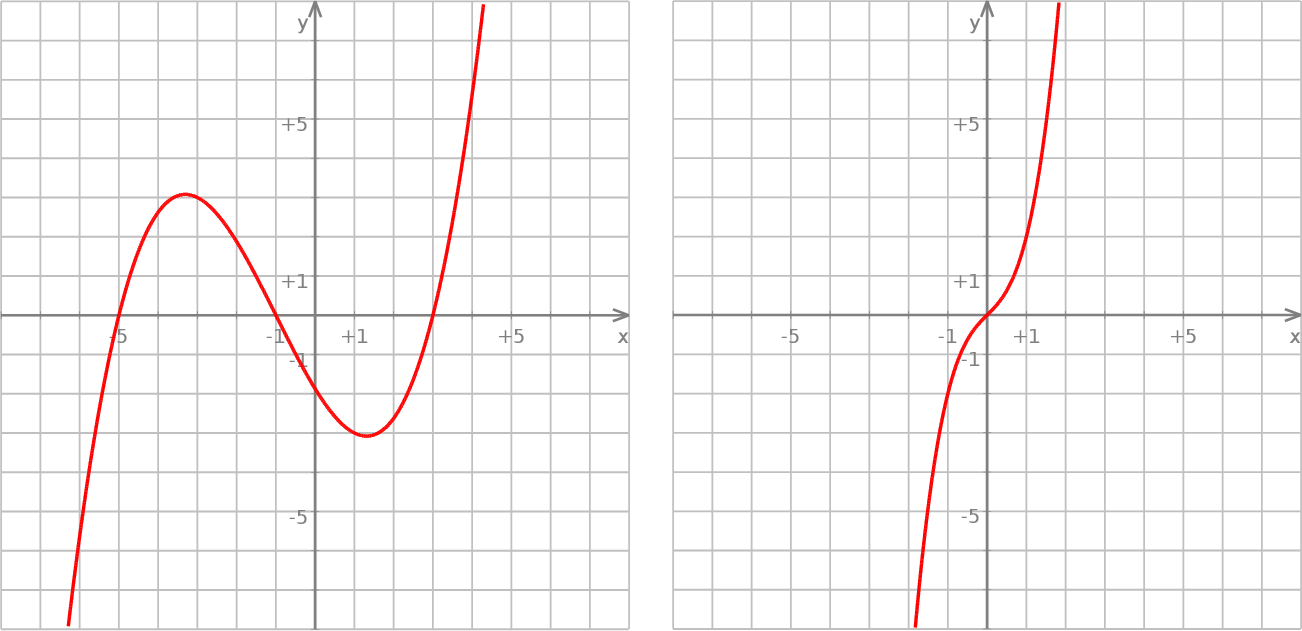
Prawy wykres pokazuje, że może się zdarzyć, że dołków/górek jest mniej (jest to wykres 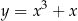 ).
).
Rozwiążmy nierówność: 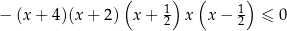 .
.
Szkicujemy sobie wykres: jest to wielomian stopnia 5 z ujemnym współczynnikiem przy 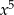 , zatem zaczyna się w lewym górnym rogu i biegnie do prawego dolnego. Po drodze musi przecinać oś
, zatem zaczyna się w lewym górnym rogu i biegnie do prawego dolnego. Po drodze musi przecinać oś 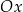 w punktach
w punktach 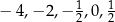 .
.
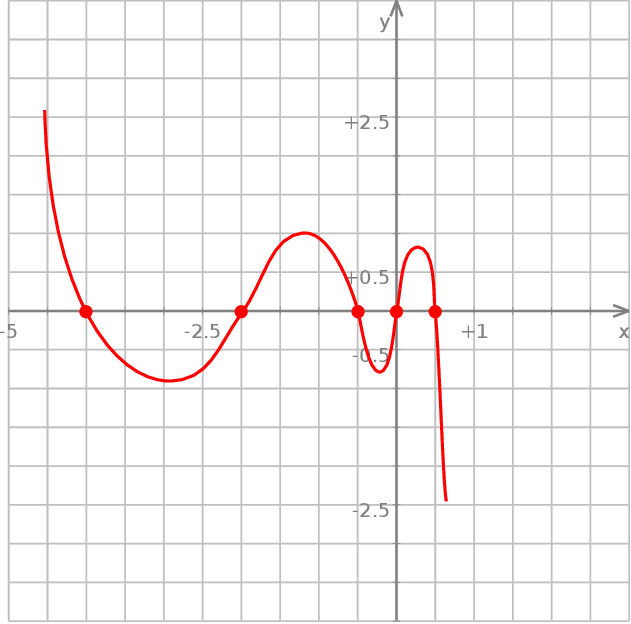
Z wykresu łatwo odczytać, że rozwiązaniem nierówności jest zbiór 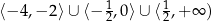 . Podkreślmy jeszcze, że to co naszkicowaliśmy nie jest wykresem lewej strony nierówności – jest to jedynie szkic przebiegu tego wykresu. Do rozwiązania nierówności nic nam jednak więcej nie potrzeba.
. Podkreślmy jeszcze, że to co naszkicowaliśmy nie jest wykresem lewej strony nierówności – jest to jedynie szkic przebiegu tego wykresu. Do rozwiązania nierówności nic nam jednak więcej nie potrzeba.
Działania na wielomianach Proste działania na wielomianach są dość oczywiste: dodajemy je i odejmujemy grupując współczynniki przy jednakowych potęgach  . Mnożąc wielomiany wymnażamy nawiasy metodą każdy z każdym. Oczywiście możemy przy tym stosować wzory skróconego mnożenia.
. Mnożąc wielomiany wymnażamy nawiasy metodą każdy z każdym. Oczywiście możemy przy tym stosować wzory skróconego mnożenia.
Uzasadnijmy, że dla dowolnej liczby całkowitej  liczba
liczba 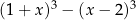 jest podzielna przez 3.
jest podzielna przez 3.
Liczymy (korzystamy ze wzoru na różnicę sześcianów).
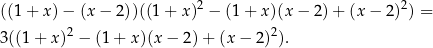
Oczywiście liczba ta dzieli się przez 3.
Jaki jest współczynnik przy 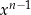 wielomianu
wielomianu 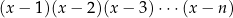 ?
?
W jaki sposób możemy otrzymać 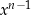 wymnażając podane nawiasy? Jedyny sposób to z jednego z nawiasów wybrać liczbę, a z pozostałych
wymnażając podane nawiasy? Jedyny sposób to z jednego z nawiasów wybrać liczbę, a z pozostałych  (bo
(bo  -ów ma być
-ów ma być 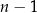 ). W zależności od nawiasu, z którego wybierzemy liczbę otrzymamy składniki
). W zależności od nawiasu, z którego wybierzemy liczbę otrzymamy składniki
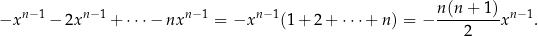
Warto zapamiętać, że przy mnożeniu wielomianów stopnie wielomianów dodają się, co możemy symbolicznie zapisać wzorem
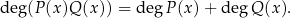
Wyznaczmy wielomian 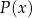 , tak aby spełniona była równość
, tak aby spełniona była równość
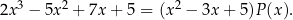
Skoro iloczyn składników z prawej strony ma mieć stopień 3, a jeden z nich ma stopień dwa, to drugi musi być stopnia 1. Szukamy zatem wielomianu postaci 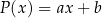 . Wymnażamy teraz prawą stronę.
. Wymnażamy teraz prawą stronę.
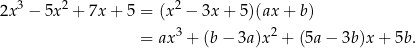
Porównując współczynniki po obu stronach równości otrzymujemy od razu 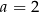 i
i 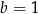 , czyli
, czyli 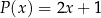 .
.
Inną bardzo użyteczną operacją jest dzielenie wielomianów, czemu poświęcony jest osobny poradnik.

