Zestaw użytkownika nr 3577_5308

Zestaw użytkownika
nr 3577_5308

Zadanie 1

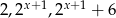Znajdź , dla którego liczby x+ 1 x+1 2,2 ,2 + 6 w podanej kolejności tworzą ciąg arytmetyczny.

Zadanie 2

50 wyraz ciągu arytmetycznego 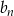jest równy 5. Oblicz 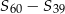S 60 − S39 , gdzie 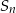oznacza sumę początkowych wyrazów ciągu .

Zadanie 3

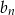Iloraz ciągu geometrycznego 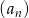(an) równy jest 3, a suma odwrotności wyrazu pierwszego i drugiego wynosi 18.

Oblicz pierwszy wyraz ciągu .
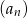Podaj wzór na wyraz ogólny ciągu .

Zadanie 4

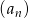Sprawdź, czy ciąg o wyrazach 2, 6, 18, 36 jest geometryczny.
Wyznacz cztery początkowe wyrazy ciągu geometrycznego, jeśli: .
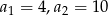Jaką liczbą musi być , aby liczby: 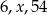tworzyły ciąg geometryczny.

Zadanie 5

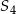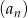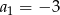Oblicz sumę pierwszych wyrazów ciągu geometrycznego, jeżeli a1 = − 3 ,q = n = 4 .

Zadanie 6

Oblicz sumę ośmiu początkowych wyrazów rosnącego ciągu geometrycznego, w którym 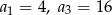a1 = 4, a3 = 16 .

Zadanie 7

Między liczby -5 i 49 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.

Zadanie 8

Określ wzorem rekurencyjnym ciąg którego pierwszy i drugi wyraz jest równy 3, a każdy następny jest iloczynem dwóch poprzednich.

Zadanie 9

Ciągiem Fibonacciego nazywamy ciąg, którego dwa pierwsze wyrazy są równe 1, a każdy kolejny jest sumą dwóch poprzednich. Jaką liczbą, parzystą czy nieparzystą, jest 528 wyraz ciągu Fibonacciego? Odpowiedź uzasadnij.

Zadanie 10

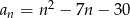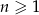Ile wyrazów ciągu o wyrazie ogólnym 2 an = n − 7n − 30 , dla n ≥ 1 , jest liczbami ujemnymi?

Arkusz Wersja PDF