Zestaw użytkownika nr 3584_6276
Zestaw użytkownika
nr 3584_6276
Dana jest funkcja liniowa 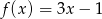 .
.
- Rozwiąż nierówność
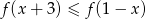 .
. - Podaj maksymalne przedziały monotoniczności funkcji
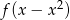 .
.
Dla jakich wartości parametru 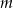 funkcja
funkcja 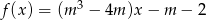 jest:
jest:
- malejąca
- nieparzysta
- parzysta
Znajdź wszystkie funkcje liniowe określone na zbiorze 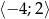 , których zbiorem wartości jest przedział
, których zbiorem wartości jest przedział 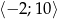 .
.
Wyznacz wzór funkcji liniowej 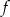 wiedząc, że zbiorem rozwiązań nierówności
wiedząc, że zbiorem rozwiązań nierówności 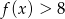 jest przedział
jest przedział 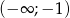 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 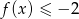 jest przedział
jest przedział 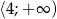 .
.
Wiadomo, że funkcja liniowa 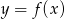 przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy
przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy 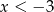 . Ponadto,
. Ponadto, 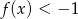 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 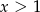 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 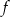 .
.
Wyznacz najmniejszą i największą wartość funkcji 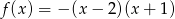 w przedziale
w przedziale 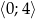 .
.
Wyznacz wzór funkcji 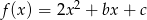 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 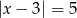 .
.
Wyznacz najmniejszą i największą wartość funkcji 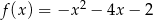 w przedziale
w przedziale 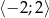 .
.
Określ zbiór wartości funkcji: 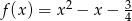 . Dla jakich argumentów funkcja przyjmuje wartości ujemne?
. Dla jakich argumentów funkcja przyjmuje wartości ujemne?

