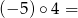Zestaw użytkownika nr 3590_2206
matura rozszerzenie liczby
Korzystając ze wzoru
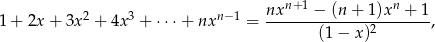
który jest prawdziwy dla dowolnej liczby naturalnej  i dowolnej liczby
i dowolnej liczby 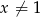 , wykaż, że
, wykaż, że
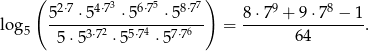
Wykaż, że liczba 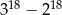 jest podzielna przez 19.
jest podzielna przez 19.
Uzasadnij, że liczba 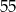 jest dzielnikiem liczby 31!, i że liczba 37 nie jest dzielnikiem liczby 31!.
jest dzielnikiem liczby 31!, i że liczba 37 nie jest dzielnikiem liczby 31!.
Niech 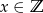 . Wykaż, że wyrażenie
. Wykaż, że wyrażenie 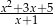 przyjmuje wartość całkowitą tylko dla czterech wartości
przyjmuje wartość całkowitą tylko dla czterech wartości  . Podaj te liczby.
. Podaj te liczby.
Wykaż, że kwadrat liczby całkowitej dającej z dzielenia przez 3 resztę 2, przy dzieleniu przez 3 daje resztę 1.
Wiadomo, że liczba  jest rozwiązaniem równania
jest rozwiązaniem równania 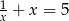 , gdzie
, gdzie 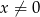 . Nie wyznaczając
. Nie wyznaczając  , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 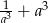 .
.
Wykaż, że jeżeli przy dzieleniu przez 7 jedna liczba daję resztę 3, a druga resztę 4, to iloczyn tych liczb daje przy dzieleniu przez 7 resztę 5.
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 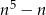 jest podzielna przez 30.
jest podzielna przez 30.
Wiedząc, że liczba  jest rozwiązaniem równania
jest rozwiązaniem równania 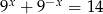 , wyznacz wartość wyrażenia
, wyznacz wartość wyrażenia 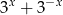 .
.
Dla dowolnych liczb rzeczywistych  i
i 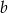 określamy liczby
określamy liczby 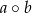 i
i 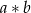 w następujący sposób:
w następujący sposób:
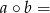 liczba nie mniejsza spośród liczb
liczba nie mniejsza spośród liczb  i
i 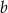 ,
, 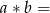 liczba nie większa spośród liczb a i b.
liczba nie większa spośród liczb a i b.
Na przykład: 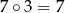 ,
, 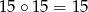 ,
, 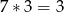 ,
, 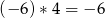 ,
, 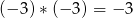 .
.
Oblicz