Zestaw użytkownika nr 3630_2220
Zestaw użytkownika
nr 3630_2220
Suma drugiego, czwartego i szóstego wyrazu ciągu arytmetycznego jest równa 42, zaś suma kwadratów wyrazów drugiego i trzeciego jest równa 185. Wyznacz pierwszy wyraz i różnicę tego ciągu.
Dany jest ciąg arytmetyczny 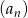 dla
dla 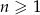 , w którym
, w którym 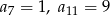 .
.
- Oblicz pierwszy wyraz
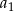 i różnicę
i różnicę  ciągu
ciągu 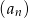 .
. - Sprawdź, czy ciąg
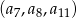 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 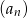 miała wartość najmniejszą.
miała wartość najmniejszą.
Dany jest ciąg 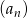 mający tę własność, że dla każdej liczby naturalnej
mający tę własność, że dla każdej liczby naturalnej  suma
suma  początkowych wyrazów tego ciągu jest równa
początkowych wyrazów tego ciągu jest równa 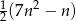 . Oblicz dwudziesty wyraz tego ciągu. Wykaż, że
. Oblicz dwudziesty wyraz tego ciągu. Wykaż, że 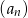 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 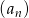 wyraża się wzorem
wyraża się wzorem 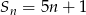 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz ciągu
-ty wyraz ciągu 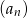 dla
dla 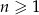 .
.
Długości boków trójkąta tworzą ciąg geometryczny. Jaki warunek spełniać musi iloraz tego ciągu?
Długości boków trójkąta tworzą trzy kolejne wyrazy ciągu arytmetycznego o różnicy 1. Oblicz długości boków tego trójkąta, jeśli jego pole wynosi 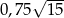 .
.
Wyznacz liczby  oraz
oraz 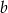 , dla których ciąg
, dla których ciąg 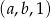 jest ciągiem arytmetycznym, natomiast ciąg
jest ciągiem arytmetycznym, natomiast ciąg 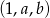 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.
Pierwszy wyraz ciągu arytmetycznego jest równy -5, a suma dwudziestu początkowych wyrazów tego ciągu jest równa 1230. Wyznacz różnicę tego ciągu.
Pierwszy wyraz malejącego ciągu arytmetycznego 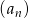 jest równy 3, a iloczyn wyrazów czwartego i piątego równy jest 15. Oblicz różnicę ciągu
jest równy 3, a iloczyn wyrazów czwartego i piątego równy jest 15. Oblicz różnicę ciągu 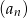 oraz sumę 14 jego początkowych wyrazów.
oraz sumę 14 jego początkowych wyrazów.
Piąty wyraz ciągu arytmetycznego jest równy 26, a suma pięciu początkowych wyrazów tego ciągu jest równa 70. Oblicz pierwszy wyraz tego ciągu.
Dany jest ciąg arytmetyczny o pierwszym wyrazie 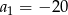 i różnicy
i różnicy 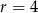 . Wyznacz liczbę
. Wyznacz liczbę  , dla której suma częściowa
, dla której suma częściowa 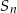 jest równa 780.
jest równa 780.

