Zestaw użytkownika nr 3717_6241
Stereometria
Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa  . Kąt między krawędzią boczną i krawędzią podstawy ma miarę
. Kąt między krawędzią boczną i krawędzią podstawy ma miarę 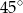 . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa  . Kąt między krawędzią boczną i krawędzią podstawy ma miarę
. Kąt między krawędzią boczną i krawędzią podstawy ma miarę 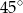 . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
Podstawą ostrosłupa jest trójkąt prostokątny, którego kąt ostry ma miarę 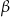 . Wszystkie krawędzie boczne mają długość
. Wszystkie krawędzie boczne mają długość 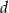 i są nachylone do płaszczyzny podstawy pod kątem o mierze
i są nachylone do płaszczyzny podstawy pod kątem o mierze  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość 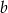 , a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę
, a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W graniastosłupie prawidłowym trójkątnym poprowadzono płaszczyznę  wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna
wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna  z płaszczyzną podstawy graniastosłupa tworzy kąt o mierze
z płaszczyzną podstawy graniastosłupa tworzy kąt o mierze 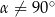 . Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę
. Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę  jest równe
jest równe 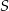 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
Odległość środka wysokości ostrosłupa prawidłowego trójkątnego od ściany bocznej jest równa 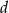 . Krawędź boczna tworzy z płaszczyzną podstawy kąt
. Krawędź boczna tworzy z płaszczyzną podstawy kąt  . Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna o długości 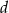 tworzy z wysokością kąt o mierze
tworzy z wysokością kąt o mierze  .
.
- Wyprowadź wzór na objętość walca.
- Oblicz tę objętość dla
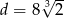 i
i 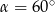 .
.
Trójkąt o bokach 3,5,7 jest podstawą graniastosłupa prostego, w który wpisano kulę. Oblicz objętość tego graniastosłupa.
Wszystkie krawędzie boczne ostrosłupa trójkątnego 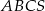 o wierzchołku
o wierzchołku 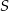 mają długość
mają długość 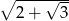 . Wiedząc, że
. Wiedząc, że 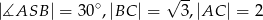 oblicz objętość tego ostrosłupa.
oblicz objętość tego ostrosłupa.
W graniastosłupie prawidłowym sześciokątnym poprowadzono płaszczyznę, która przechodzi przez dłuższą przekątną dolnej podstawy oraz przez jedną z krawędzi górnej podstawy. Płaszczyzna ta wyznacza przekrój graniastosłupa, który jest trapezem równoramiennym. Wiedząc, że w trapez ten można wpisać okrąg o promieniu 1, oblicz objętość graniastosłupa.
Liczba wszystkich przekątnych podstaw i ścian bocznych pewnego graniastosłupa jest równa 110. Oblicz, ile krawędzi ma podstawa tego graniastosłupa.
Podstawą ostrosłupa 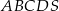 jest prostokąt
jest prostokąt 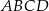 , w którym
, w którym 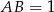 ,
, 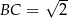 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz wartość dowolnej funkcji trygonometrycznej kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
. Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz wartość dowolnej funkcji trygonometrycznej kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
Pole ściany bocznej ostrosłupa prawidłowego czworokątnego jest równe 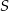 . Kąt płaski przy wierzchołku ostrosłupa ma miarę
. Kąt płaski przy wierzchołku ostrosłupa ma miarę 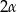 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Oblicz cosinus kąta jaki tworzą dwie ściany czworościanu foremnego. Podaj przybliżoną miarę tego kąta.
Wykaż, że jeśli wszystkie krawędzie boczne ostrosłupa trójkątnego tworzą z podstawą kąty o równych miarach to spodek wysokości ostrosłupa jest środkiem okręgu opisanego na tym trójkącie.
Oto w jaki sposób można uzasadnić, że suma odległości dowolnego punktu 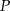 wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.
wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.
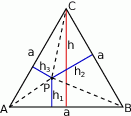
- Łączymy punkt
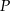 z wierzchołkami trójkąta i zapisujemy równość pól
z wierzchołkami trójkąta i zapisujemy równość pól 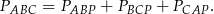
- Korzystamy ze wzoru na pole trójkąta
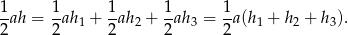
- Wnioskujemy, że
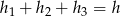 , a więc suma ta nie zależy od wyboru punktu
, a więc suma ta nie zależy od wyboru punktu 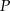 .
.
Postępując w analogiczny sposób wykaż, że suma odległości dowolnego punktu 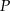 wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu
wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu 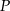 .
.
Przekrój stożka wyznaczony przez wierzchołek i cięciwę podstawy jest trójkątem równobocznym, o polu równym 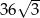 . Płaszczyzna
. Płaszczyzna  , do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej
, do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej 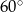 . Oblicz objętość stożka.
. Oblicz objętość stożka.
Rozwinięcie powierzchni bocznej stożka jest wycinkiem kołowym o kącie środkowym  . Kąt ten oparty jest na łuku długości
. Kąt ten oparty jest na łuku długości  . Oblicz objętość stożka.
. Oblicz objętość stożka.
Podstawą graniastosłupa prostego jest trójkąt prostokątny równoramienny. Kąt między przekątnymi, wychodzącymi z tego samego wierzchołka, dwóch prostopadłych ścian bocznych, ma miarę 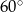 . Wiedząc, że objętość tego graniastosłupa jest równa
. Wiedząc, że objętość tego graniastosłupa jest równa 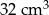 , oblicz pole powierzchni całkowitej tej bryły.
, oblicz pole powierzchni całkowitej tej bryły.
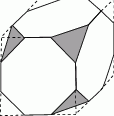
W kostce mającej kształt sześcianu o boku 1 dm ścięto wszystkie naroża w ten sposób ze wszystkie krawędzie nowopowstałej bryły mają tę samą długość. Obliczyć objętość otrzymanej bryły.
W kulę o promieniu 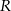 wpisano stożek. Ze środka tej kuli widać tworzącą stożka pod kątem
wpisano stożek. Ze środka tej kuli widać tworzącą stożka pod kątem  . Oblicz objętość stożka.
. Oblicz objętość stożka.
W czworościanie 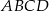 krawędź
krawędź 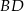 ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
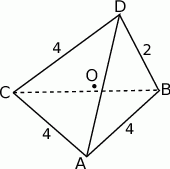
- Oblicz odległość krawędzi
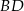 od krawędzi
od krawędzi 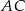 .
. - Wiedząc, że punkt
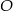 jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka
jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka 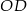 .
.
W ostrosłupie prawidłowym czworokątnym krawędź boczna tworzy z krawędzią podstawy kąta  . Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi.
. Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi.
W sferę o promieniu 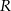 wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość
wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość 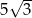 , oblicz
, oblicz 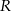 .
.
Wysokość walca wpisanego w stożek jest równa promieniowi podstawy stożka. Stosunek objętości stożka do objętości walca wynosi 8:3. Oblicz tangens kąta zawartego między wysokością a tworzącą stożka.
Podstawą ostrosłupa prawidłowego czworokątnego 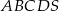 jest kwadrat
jest kwadrat 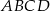 . Pole trójkąta równoramiennego
. Pole trójkąta równoramiennego 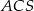 jest równe 120 oraz
jest równe 120 oraz 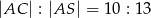 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
W ostrosłupie prawidłowym sześciokątnym pole przekroju płaszczyzną przechodzącą przez jego wysokość oraz przez dwie krawędzie boczne jest dwukrotnie większe od pola podstawy i wynosi 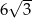 . Oblicz odległość spodka wysokości ostrosłupa od jego krawędzi bocznej.
. Oblicz odległość spodka wysokości ostrosłupa od jego krawędzi bocznej.
Trójkąt prostokątny o przyprostokątnych 15 i 20 obraca się wokół przeciwprostokątnej. Oblicz objętość i pole powierzchni całkowitej tej bryły.
Na płaskiej powierzchni położono trzy kule 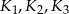 , każda o promieniu 2 tak, że kule
, każda o promieniu 2 tak, że kule 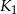 i
i 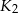 są styczne w punkcie
są styczne w punkcie 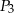 , kule
, kule 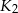 i
i 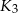 są styczne w punkcie
są styczne w punkcie 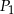 , a kule
, a kule 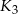 i
i 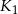 są styczne w punkcie
są styczne w punkcie 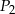 . Następnie położono na tych kulach kulę
. Następnie położono na tych kulach kulę 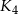 o promieniu 3, która jest styczna do kul
o promieniu 3, która jest styczna do kul 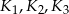 odpowiednio w punktach
odpowiednio w punktach 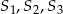 .
.
- Uzasadnij, że odcinki
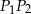 i
i 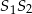 są równoległe.
są równoległe. - Oblicz obwód trapezu
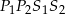 .
.
Na płaskiej powierzchni położono trzy kule 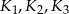 , każda o promieniu 2 tak, że kule
, każda o promieniu 2 tak, że kule 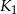 i
i 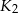 są styczne w punkcie
są styczne w punkcie 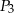 , kule
, kule 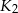 i
i 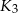 są styczne w punkcie
są styczne w punkcie 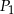 , a kule
, a kule 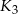 i
i 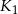 są styczne w punkcie
są styczne w punkcie 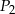 . Następnie położono na tych kulach kulę
. Następnie położono na tych kulach kulę 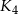 o promieniu 3, która jest styczna do kul
o promieniu 3, która jest styczna do kul 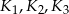 odpowiednio w punktach
odpowiednio w punktach 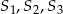 .
.
- Uzasadnij, że odcinki
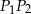 i
i 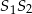 są równoległe.
są równoległe. - Oblicz obwód trapezu
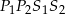 .
.
Podstawą graniastosłupa prawidłowego jest trójkąt, w którym wysokość ma długość 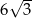 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt  taki, że
taki, że 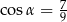 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna ma długość 18 cm i tworzy z bokiem odpowiadającym wysokości walca kąt o mierze 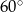 . Oblicz objętość walca.
. Oblicz objętość walca.
Oblicz objętość graniastosłupa prawidłowego trójkątnego, w którym krawędź podstawy ma długość 1, a przekątna ściany bocznej tworzy z sąsiednią ścianą kąt o mierze 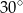 .
.
W ostrosłup prawidłowy czworokątny wpisano kulę o promieniu  . Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem
. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 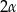 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłup prawidłowy czworokątny wpisujemy graniastosłupy prawidłowe czworokątne w ten sposób, że dolna podstawa graniastosłupa zawiera się podstawie ostrosłupa, a każdy z wierzchołków górnej podstawy należy do jednej z krawędzi bocznych ostrosłupa. Wiedząc, że każda z krawędzi ostrosłupa ma długość 6, oblicz jaka jest maksymalna możliwa powierzchnia boczna graniastosłupa.
Podstawą ostrosłupa jest romb o boku długości 18cm. Każda ze ścian bocznych tworzy z płaszczyzną podstawy kąt 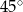 . Pole powierzchni bocznej ostrosłupa jest równe
. Pole powierzchni bocznej ostrosłupa jest równe 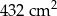 . Oblicz jego objętość.
. Oblicz jego objętość.
Tangens kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa prawidłowego czworokątnego jest równy  . Oblicz tangens nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.
. Oblicz tangens nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.
Wysokość ostrosłupa prawidłowego sześciokątnego jest równa 6 cm i stanowi  długości krawędzi podstawy.
długości krawędzi podstawy.
- Oblicz miarę kąta nachylenia ściany bocznej do podstawy.
- Oblicz objętość ostrosłupa
W ostrosłupie prawidłowym czworokątnym pole podstawy jest równe 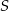 , a kąt nachylenia ściany bocznej do płaszczyzny podstawy ma miarę
, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ma miarę  . Ostrosłup przecięto płaszczyzną zawierającą krawędź boczną tego ostrosłupa i przechodzącą przez środek rozłącznej z nią krawędzi podstawy. Oblicz pole otrzymanego przekroju.
. Ostrosłup przecięto płaszczyzną zawierającą krawędź boczną tego ostrosłupa i przechodzącą przez środek rozłącznej z nią krawędzi podstawy. Oblicz pole otrzymanego przekroju.
W ostrosłupie prawidłowym czworokątnym przeciwległe krawędzie boczne są prostopadłe, a wysokość ściany bocznej poprowadzona z wierzchołka ostrosłupa ma długość 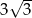 . Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej ostrosłupa.

