Zestaw użytkownika nr 3747_1593
POTĘGI, LOGARYTMYCzas pracy: 90 min.
Oblicz 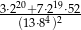 .
.
Przedstaw 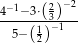 w postaci nieskracalnego ułamka zwykłego.
w postaci nieskracalnego ułamka zwykłego.
Zapisz podane wyrażenie w prostszej postaci: 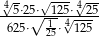 .
.
Wyrażenie 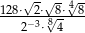 zapisz w postaci
zapisz w postaci 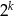 , gdzie
, gdzie 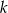 jest liczbą wymierną.
jest liczbą wymierną.
Uprość wyrażenie 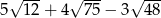 .
.
Zapisz jako potęgę liczby 3 wyrażenie
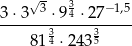
Wykaż, że liczba 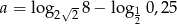 jest liczbą wymierną.
jest liczbą wymierną.
Oblicz 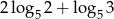 .
.
Oblicz 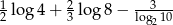 .
.
Wiadomo, że 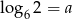 . Wyznacz
. Wyznacz 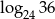 w zależności od
w zależności od  .
.
Oblicz 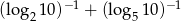 .
.
Udowodnij, że liczby 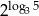 i
i 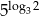 są równe.
są równe.
Wiedząc, że 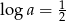 i
i 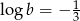 , oblicz
, oblicz 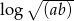 .
.
Wiadomo, że 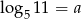 . Wykaż, że
. Wykaż, że 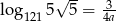 .
.
Wartość wyrażenia 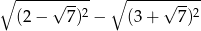 jest równa
jest równa
A) -5 B) 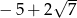 C)
C) 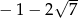 D) -1
D) -1
Czwarta potęga liczby 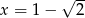 jest równa
jest równa
A) 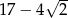 B)
B) 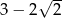 C)
C) 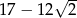 D)
D) 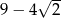
Wartość wyrażenia 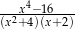 dla
dla 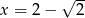 jest równa
jest równa
A) -2 B) 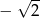 C) 2 D)
C) 2 D) 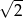
Liczby 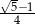 i
i 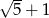 to liczby
to liczby
A) równe B) wymierne C) będące swoimi odwrotnościami D) przeciwne
Wiadomo, że 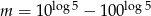 i
i 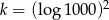 . Zatem
. Zatem
A) 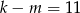 B)
B) 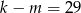 C)
C) 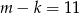 D)
D) 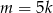
Liczba 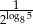 jest równa
jest równa
A) 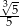 B)
B) 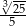 C)
C) 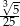 D)
D)