Zestaw użytkownika nr 3747_4271
Zestaw użytkownika
nr 3747_4271
Rozwiąż nierówność 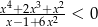 .
.
Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 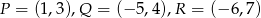 .
.
W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu.
Dany jest wielomian 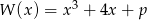 , gdzie
, gdzie 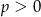 jest liczbą pierwszą. Znajdź
jest liczbą pierwszą. Znajdź 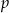 wiedząc, że
wiedząc, że 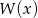 ma pierwiastek całkowity.
ma pierwiastek całkowity.
Dany jest ciąg arytmetyczny 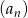 dla
dla 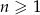 , w którym
, w którym 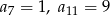 .
.
- Oblicz pierwszy wyraz
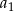 i różnicę
i różnicę  ciągu
ciągu 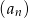 .
. - Sprawdź, czy ciąg
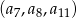 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 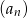 miała wartość najmniejszą.
miała wartość najmniejszą.
Wiedząc, że  jest kątem ostrym oraz
jest kątem ostrym oraz 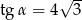 oblicz wartość wyrażenia
oblicz wartość wyrażenia 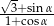 .
.
Dany jest wykres funkcji logarytmicznej 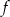 .
.
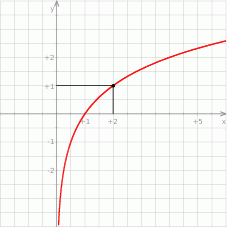
- Wyznacz wzór funkcji
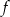 .
. - Narysuj wykres funkcji
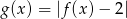 .
. - Odczytaj z rysunku zbiór argumentów, dla których wartości funkcji
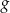 są nie mniejsze od wartości funkcji
są nie mniejsze od wartości funkcji 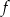 .
.
Rozwiąż nierówność 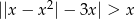 .
.
Proste 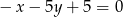 i
i 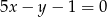 przecinają się pod kątem o mierze
przecinają się pod kątem o mierze
A) 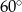 B)
B) 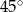 C)
C) 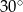 D)
D) 
Korzystając ze wzoru
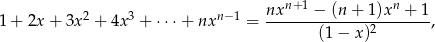
który jest prawdziwy dla dowolnej liczby naturalnej  i dowolnej liczby
i dowolnej liczby 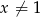 , wykaż, że
, wykaż, że
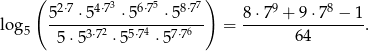
Jeżeli 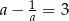 to liczba
to liczba 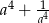 jest równa
jest równa
A) 123 B) 121 C) 81 D) 119
Ze zbioru 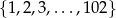 losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?
losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?
Podstawą ostrosłupa 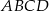 jest trójkąt
jest trójkąt 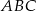 . Krawędź
. Krawędź 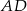 jest wysokością ostrosłupa (zobacz rysunek).
jest wysokością ostrosłupa (zobacz rysunek).
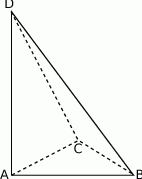
Oblicz objętość ostrosłupa 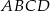 , jeśli wiadomo, że
, jeśli wiadomo, że 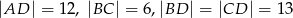 .
.
Dany jest ciąg 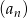 jest określony wzorem
jest określony wzorem 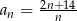 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa
A) 5 B) 2 C) 4 D) 3
Kąt  jest ostry oraz
jest ostry oraz 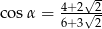 . Wtedy
. Wtedy 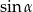 jest równy
jest równy
A) 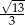 B)
B) 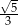 C)
C) 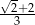 D)
D) 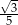
Dane są 2 koła styczne zewnętrznie o promieniach 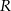 i
i  (
(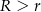 ) oraz środkach
) oraz środkach 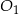 i
i 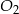 . Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach
. Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach 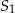 i
i 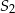 odpowiednio (
odpowiednio (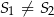 ). Oblicz pole trójkąta
). Oblicz pole trójkąta 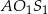 , gdzie
, gdzie 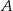 jest punktem przecięcia się prostych
jest punktem przecięcia się prostych 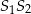 i
i 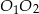 .
.