Zestaw użytkownika nr 3762_1808
funkcja wykładnicza i logarytmiczna
Wyznacz wszystkie wartości parametru 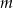 , dla których dziedziną funkcji
, dla których dziedziną funkcji
![2 2 f(x ) = log[(m + m − 6)x + (m − 2)x + 1]](https://img.zadania.info/zad/2939774/HzadT1x.gif)
jest zbiór wszystkich liczb rzeczywistych.
Wyznacz dziedzinę funkcji 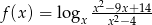 .
.
Wyznacz te wartości parametru 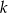 , dla których dziedziną funkcji
, dla których dziedziną funkcji 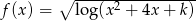 jest zbiór liczb rzeczywistych.
jest zbiór liczb rzeczywistych.
Określ dziedzinę funkcji 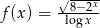 .
.
Wyznacz dziedzinę funkcji 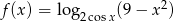 i zapisz ją w postaci sumy przedziałów liczbowych.
i zapisz ją w postaci sumy przedziałów liczbowych.
Wyznacz dziedzinę funkcji 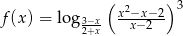
Oblicz wartość funkcji 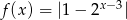 dla argumentu
dla argumentu
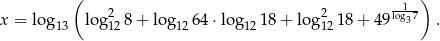
Wykaż, że liczba 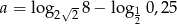 jest liczbą wymierną.
jest liczbą wymierną.
Oblicz 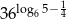 .
.
Udowodnij, że jeśli liczby dodatnie  i
i 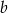 spełniają warunek
spełniają warunek 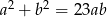 , to
, to 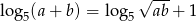 .
.
Oblicz 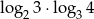 .
.
Uporządkuj rosnąco liczby 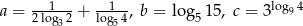 .
.
Oblicz wartość wyrażenia 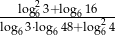 .
.
Wykaż, że dla liczb spełniających odpowiednie założenia (podaj te założenia) prawdziwy jest wzór: 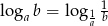 .
.
Udowodnij, że liczby 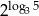 i
i 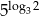 są równe.
są równe.
Zaznacz w układzie współrzędnych zbiór punktów 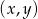 , dla których współrzędne spełniają nierówność
, dla których współrzędne spełniają nierówność 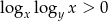 .
.
Rozwiąż graficznie nierówność 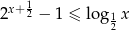 .
.
Zaznacz w układzie współrzędnych zbiór wszystkich punktów 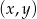 , których współrzędne spełniają nierówność
, których współrzędne spełniają nierówność 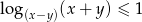 .
.
W prostokątnym układzie współrzędnych zaznacz zbiór wszystkich punktów płaszczyzny, których współrzędne spełniają warunek: 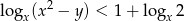 .
.
Dana jest funkcja 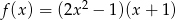
- Rozwiąż równanie
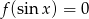 .
. - Rozwiąż nierówność
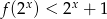 .
.
Rozwiąż równanie 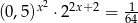 .
.
Dane jest równanie 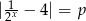 z parametrem
z parametrem 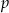 . Wyznacz liczbę rozwiązań tego równania w zależności od parametru
. Wyznacz liczbę rozwiązań tego równania w zależności od parametru 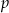 .
.
Funkcja 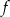 dana jest wzorem
dana jest wzorem
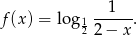
Określ dziedzinę funkcji 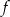 i naszkicuj jej wykres w przedziale
i naszkicuj jej wykres w przedziale 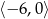 .
.
Dana jest funkcja 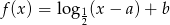 . Wyznacz wartości parametrów
. Wyznacz wartości parametrów  i
i 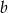 , jeśli wiesz, że dziedziną funkcji jest przedział
, jeśli wiesz, że dziedziną funkcji jest przedział 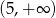 i do wykresu należy punkt
i do wykresu należy punkt 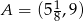 . Podaj wzór tej funkcji.
. Podaj wzór tej funkcji.
Naszkicuj wykresy funkcji 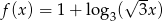 i
i 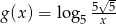 , gdzie
, gdzie 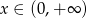 . Odczytaj z wykresów zbiór rozwiązań nierówności
. Odczytaj z wykresów zbiór rozwiązań nierówności 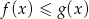 .
.
Dana jest funkcja 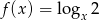 .
.
- Określ dziedzinę funkcji
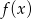 .
. - Naszkicuj wykres funkcji
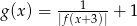 .
. - Odczytaj z wykresu maksymalne przedziały monotoniczności funkcji
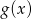 .
.
Wykres funkcji 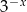 przesunięto o wektor
przesunięto o wektor ![→ v = [3,a]](https://img.zadania.info/zad/3436166/HzadT1x.gif) otrzymując wykres funkcji
otrzymując wykres funkcji 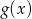 . Wiedząc, że wykresy funkcji
. Wiedząc, że wykresy funkcji 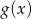 i
i 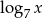 przecinają się na osi
przecinają się na osi 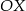 oblicz
oblicz  . Narysuj wykres funkcji
. Narysuj wykres funkcji 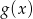 .
.

