Zestaw użytkownika nr 3783_9630

Geometria analitycznaSprawdzian5 Listopada 2012Czas pracy: 90 min.Suma punktów: 35

Zadanie 1

(5 pkt)

Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 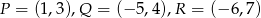P = (1,3),Q = (− 5,4),R = (− 6,7) .

Zadanie 2

(5 pkt)

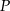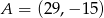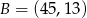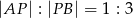Wyznacz współrzędne punktu , który dzieli odcinek o końcach A = (29,− 15) i B = (45,13) w stosunku |AP | : |PB | = 1 : 3 .

Zadanie 3

(5 pkt)

Dla jakich wartości parametru 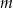równanie 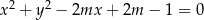2 2 x + y − 2mx + 2m − 1 = 0 opisuje okrąg?

Podaj wspórzędne środka i długość promienia okręgu.
Dla jakich wartości parametru 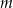okrąg ten jest styczny do prostej o równaniu ?

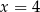Zadanie 4

(5 pkt)

Znajdź równania stycznych do okręgu 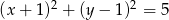2 2 (x+ 1) + (y − 1 ) = 5 poprowadzonych z punktu A = (2,0) .

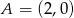Zadanie 5

(5 pkt)

Dany jest ciąg punktów 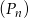(Pn) na płaszczyźnie, których współrzędne dane są wzorem 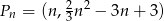Pn = (n, 23n 2 − 3n + 3) , gdzie 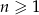n ≥ 1 . Wyznacz tę wartość , dla której odległość punktu 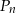od prostej 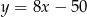y = 8x − 50 jest najmniejsza z możliwych.

Zadanie 6

(5 pkt)

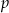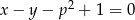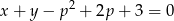Dla jakich wartości parametru proste 2 x − y − p + 1 = 0 i x + y − p 2 + 2p + 3 = 0 przecinają się w punkcie należącym do wnętrza prostokąta o wierzchołkach A = (4,− 1) , B = (10,− 1) , C = (10,2 ) , D = (4,2 ) ?

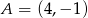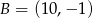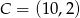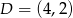Zadanie 7

(5 pkt)

Wyznacz taki punkt 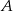na prostej 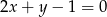2x + y − 1 = 0 , by suma kwadratów jego odległości od osi układu była najmniejsza.

Rozwiąż on-line Arkusz Wersja PDF