Zestaw użytkownika nr 3786_1608
Zestaw użytkownika
nr 3786_1608
Rozwiąż równanie 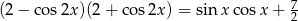 w przedziale
w przedziale 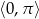 .
.
Rozwiąż równanie 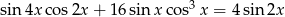 w przedziale
w przedziale 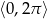 .
.
Rozwiąż równanie 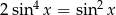 .
.
Rozwiąż równanie 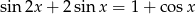 .
.
Rozwiąż równanie 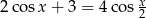 .
.
Rozwiąż równanie 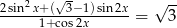 .
.
Wyznacz wszystkie rozwiązania równania 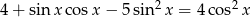 należące do przedziału
należące do przedziału 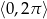 .
.
Dana jest funkcja 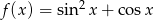 dla
dla 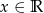 .
.
- Rozwiąż równanie
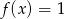 w przedziale
w przedziale 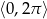 .
. - Wyznacz największą wartość funkcji
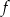 .
.
Wyznacz wszystkie wartości parametru 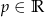 , dla których równanie
, dla których równanie 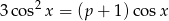 ma w przedziale
ma w przedziale 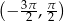 tylko trzy różne rozwiązania, z których dwa są ujemne, a jedno dodatnie.
tylko trzy różne rozwiązania, z których dwa są ujemne, a jedno dodatnie.
Wyznacz zbiór wartości parametru 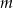 , dla których równanie:
, dla których równanie: 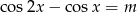 ma rozwiązania.
ma rozwiązania.
Dla jakich wartości parametru  suma kwadratów różnych pierwiastków równania
suma kwadratów różnych pierwiastków równania
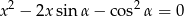
jest równa 3?
Posługując się wykresem funkcji 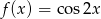 dla
dla 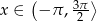 , rozwiąż nierówność
, rozwiąż nierówność 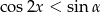 wiedząc, że miara kąta
wiedząc, że miara kąta  jest równa mierze łukowej kąta środkowego okręgu opartego na
jest równa mierze łukowej kąta środkowego okręgu opartego na 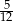 okręgu.
okręgu.
Rozwiąż nierówność 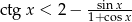 , gdzie
, gdzie 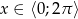 ;
;
Rozwiąż nierówność 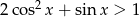 , gdzie
, gdzie 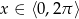 .
.
Rozwiąż nierówność 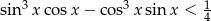 , gdzie
, gdzie 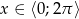 .
.
Rozwiąż nierówność 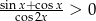 , gdzie
, gdzie 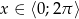 .
.
Rozwiąż nierówność 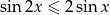 .
.
Rozwiąż nierówność: 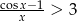 dla
dla 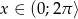 .
.
Wykaż, że jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 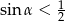 to
to 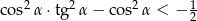 .
.
Wykaż, że dla każdej liczby 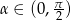 zachodzi nierówność
zachodzi nierówność 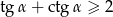 .
.

