Zestaw użytkownika nr 3792_5152
Zestaw użytkownika
nr 3792_5152
Oceń, czy liczba 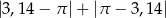 jest wymierna, czy niewymierna.
jest wymierna, czy niewymierna.
Na rysunku przedstawiony jest wykres funkcji 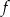 określonej wzorem
określonej wzorem 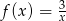 dla
dla 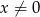 .
.
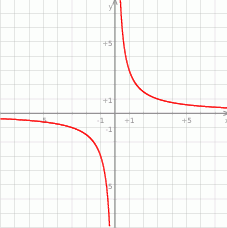
Wykres ten przesunięto o 2 jednostki w górę wzdłuż osi 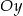 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 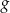 o wzorze
o wzorze 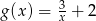 dla
dla 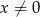 .
.
- Narysuj wykres funkcji
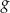 .
. - Oblicz największą wartość funkcji
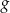 w przedziale
w przedziale 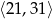 .
. - Podaj, o ile jednostek wzdłuż osi
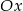 należy przesunąć wykres funkcji
należy przesunąć wykres funkcji 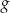 , aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
, aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
Dany jest ciąg arytmetyczny 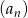 dla
dla 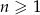 , w którym
, w którym 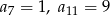 .
.
- Oblicz pierwszy wyraz
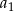 i różnicę
i różnicę  ciągu
ciągu 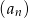 .
. - Sprawdź, czy ciąg
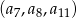 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 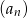 miała wartość najmniejszą.
miała wartość najmniejszą.
Rozwiąż algebraicznie układ równań 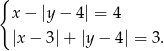
Wyznacz liczbę rozwiązań równania 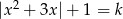 w zależności od parametru
w zależności od parametru 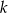 .
.
Naszkicuj wykres funkcji 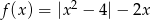 . Określ liczbę rozwiązań równania
. Określ liczbę rozwiązań równania 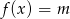 w zależności od wartości parametru
w zależności od wartości parametru 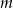 .
.
Ramiona kąta ostrego o mierze 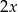 przecięto prostą
przecięto prostą 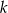 prostopadłą do dwusiecznej kąta, która jest odległa o
prostopadłą do dwusiecznej kąta, która jest odległa o 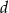 od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej
od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej 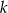 . Oblicz odległość środków tych okręgów.
. Oblicz odległość środków tych okręgów.
Dla jakich wartości parametru 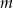 funkcja
funkcja 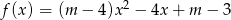 ma dwa miejsca zerowe, z których jedno jest mniejsze od 1, a drugie większe od 1?
ma dwa miejsca zerowe, z których jedno jest mniejsze od 1, a drugie większe od 1?
Rozwiąż nierówność 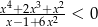 .
.
W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu opisanego ma długość 19 cm. Oblicz pole tego trójkąta.

