Zestaw użytkownika nr 3867_8209
Zestaw użytkownika
nr 3867_8209
Zadanie 1
Wykaż, że jeśli 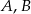 są dowolnymi zdarzeniami przestrzeni
są dowolnymi zdarzeniami przestrzeni 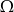 , to
, to 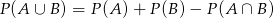 .
.
Zadanie 2
Wiadomo, że 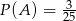 ,
, 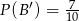 ,
, 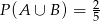 . Oblicz
. Oblicz 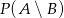 i
i 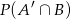 .
.
Zadanie 3
Wiadomo że 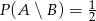 ,
, 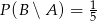 ,
, 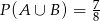 . Oblicz
. Oblicz 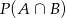 .
.
Zadanie 4
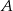 i
i 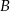 są takimi zdarzeniami losowymi zawartymi w
są takimi zdarzeniami losowymi zawartymi w 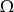 , że
, że 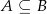 oraz
oraz 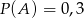 i
i 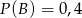 . Oblicz prawdopodobieństwo
. Oblicz prawdopodobieństwo 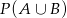 .
.
Zadanie 5
Wiadomo, że zdarzenia 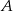 i
i 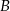 są niezależne oraz
są niezależne oraz 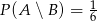 ,
, 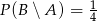 . Oblicz
. Oblicz 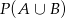 .
.
Zadanie 6
Dane są dwa takie zdarzenia 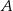 i
i 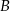 , że
, że 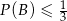 i
i 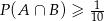 . Czy może zachodzić równość
. Czy może zachodzić równość 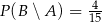 ? Odpowiedź uzasadnij.
? Odpowiedź uzasadnij.
Zadanie 7
Niech 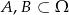 będą zdarzeniami losowymi, takimi że
będą zdarzeniami losowymi, takimi że 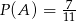 i
i 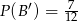 . Uzasadnij, że
. Uzasadnij, że 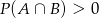 .
.

