Zestaw użytkownika nr 3914_5019
Zestaw użytkownika
nr 3914_5019
Wyznacz wzór funkcji 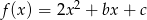 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 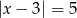 .
.
Wyznacz wzór funkcji 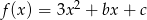 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 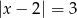 .
.
Wyznacz wszystkie całkowite wartości 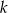 , dla których funkcja
, dla których funkcja 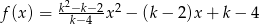 osiąga minimum i ma dwa różne miejsca zerowe.
osiąga minimum i ma dwa różne miejsca zerowe.
Dana jest funkcja kwadratowa 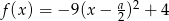
- Dla
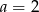 wyznacz postać iloczynową tej funkcji.
wyznacz postać iloczynową tej funkcji. - Dla
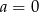 wyznacz te argumenty, dla których funkcja osiąga wartości ujemne.
wyznacz te argumenty, dla których funkcja osiąga wartości ujemne. - Wyznacz
 tak, aby osią symetrii wykresu funkcji była prosta o równaniu
tak, aby osią symetrii wykresu funkcji była prosta o równaniu 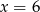 .
.
Jednym z miejsc zerowych funkcji kwadratowej 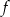 jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to
jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to 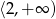 . Największa wartość funkcji
. Największa wartość funkcji 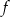 w przedziale
w przedziale 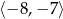 jest równa
jest równa 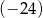 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 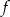 i narysuj jej wykres.
i narysuj jej wykres.
Zbiorem wartości funkcji kwadratowej 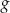 jest przedział
jest przedział 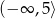 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 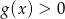 jest przedział
jest przedział 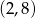 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 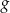 .
.
Napisz wzór i narysuj wykres funkcji 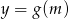 , która każdej liczbie rzeczywistej
, która każdej liczbie rzeczywistej 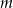 przyporządkowuje najmniejszą wartość funkcji kwadratowej
przyporządkowuje najmniejszą wartość funkcji kwadratowej 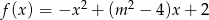 w przedziale
w przedziale 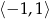 .
.
Znajdź taką wartość parametru 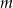 , aby największa wartość funkcji
, aby największa wartość funkcji 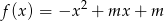 była najmniejsza z możliwych.
była najmniejsza z możliwych.
Dany jest trójmian kwadratowy 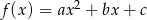 .
.
- Dla
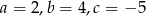 wyznacz największą i najmniejszą wartość tego trójmianu w przedziale
wyznacz największą i najmniejszą wartość tego trójmianu w przedziale 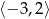 .
. - Wyznacz wzór trójmianu w postaci iloczynowej, jeśli wiadomo, że ma on miejsca zerowe
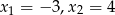 , a do jego wykresu należy punkt
, a do jego wykresu należy punkt 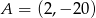 .
.
Funkcja 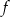 określona jest wzorem
określona jest wzorem 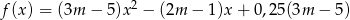 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 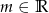 , dla których najmniejsza wartość funkcji
, dla których najmniejsza wartość funkcji 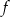 jest liczbą dodatnią.
jest liczbą dodatnią.
Funkcja kwadratowa 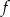 ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu -4, a do jej wykresu należy punkt
ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu -4, a do jej wykresu należy punkt 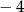 . Napisz wzór funkcji
. Napisz wzór funkcji 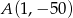 w postaci ogólnej.
w postaci ogólnej.
Dana jest funkcja 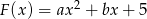 . Wyznacz
. Wyznacz  i
i 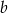 wiedząc, że
wiedząc, że 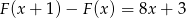 .
.
Jedynym miejscem zerowym funkcji kwadratowej 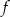 jest liczba 2. Wykres funkcji
jest liczba 2. Wykres funkcji 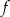 przecina oś
przecina oś 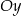 w punkcie o współrzędnych
w punkcie o współrzędnych 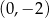 . Wyznacz wzór tej funkcji w postaci ogólnej.
. Wyznacz wzór tej funkcji w postaci ogólnej.
Wyznacz wszystkie wartości parametru 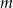 , dla których funkcja
, dla których funkcja 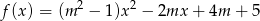 jest rosnąca w przedziale
jest rosnąca w przedziale 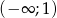 i malejąca w przedziale
i malejąca w przedziale 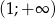 .
.
Liczba 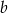 jest największą liczbą całkowitą, dla której najmniejsza wartość funkcji
jest największą liczbą całkowitą, dla której najmniejsza wartość funkcji 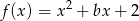 jest większa od -3. Wyznacz liczbę
jest większa od -3. Wyznacz liczbę 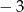 .
.
Funkcja kwadratowa określona wzorem 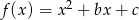 osiąga wartości ujemne wtedy i tylko wtedy, gdy
osiąga wartości ujemne wtedy i tylko wtedy, gdy 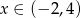 .
.
- Wyznacz wartości współczynników
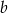 i
i  .
. - Oblicz, dla jakich argumentów
 , wartości funkcji
, wartości funkcji 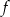 są mniejsze od wartości funkcji kwadratowej
są mniejsze od wartości funkcji kwadratowej 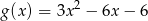 .
. - Rozwiąż równanie
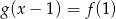 .
.
Wyznacz te wartości parametru 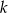 , dla których funkcja
, dla których funkcja 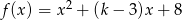 jest malejąca w przedziale
jest malejąca w przedziale 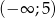 i rosnąca w przedziale
i rosnąca w przedziale 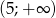 .
.
Funkcja kwadratowa 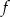 określona jest wzorem
określona jest wzorem 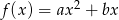 . Wiadomo, że
. Wiadomo, że 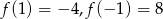 . Określ, dla jakich argumentów spełniona jest nierówność
. Określ, dla jakich argumentów spełniona jest nierówność 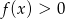 .
.
Funkcja 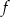 określona wzorem
określona wzorem 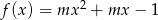 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 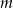 , dla których:
, dla których:
- funkcja
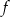 przyjmuje tylko wartości ujemne,
przyjmuje tylko wartości ujemne, - zbiorem wartości funkcji
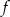 jest przedział
jest przedział 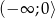 .
.
Wyznacz współczynniki funkcji kwadratowej 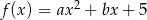 wiedząc, że
wiedząc, że 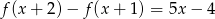 .
.
Dane są dwie funkcje kwadratowe 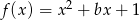 oraz
oraz 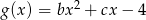 , gdzie
, gdzie 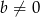 . Wyznacz wszystkie wartości parametrów
. Wyznacz wszystkie wartości parametrów 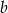 i
i  tak, aby funkcja
tak, aby funkcja 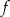 miała jedno miejsce zerowe i jednocześnie funkcja
miała jedno miejsce zerowe i jednocześnie funkcja 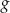 przyjmowała wartości ujemne dla każdego
przyjmowała wartości ujemne dla każdego 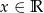 .
.
Funkcja kwadratowa 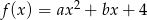 , osiąga wartości ujemne wtedy i tylko wtedy, gdy
, osiąga wartości ujemne wtedy i tylko wtedy, gdy 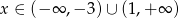 .
.
- Wyznacz wartości współczynników
 i
i 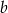 .
. - Napisz postać kanoniczną funkcji
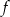 .
. - Podaj wzór funkcji kwadratowej
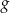 , której wykres otrzymamy przesuwając wykres funkcji
, której wykres otrzymamy przesuwając wykres funkcji 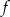 o wektor
o wektor ![→ u = [2,− 130]](https://img.zadania.info/zad/9353293/HzadT7x.gif) .
. - Wyznacz te argumenty
 , dla których
, dla których 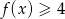 .
.
Funkcja 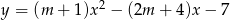 jest malejąca w zbiorze
jest malejąca w zbiorze 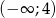 i rosnąca w zbiorze
i rosnąca w zbiorze 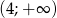 . Wyznacz parametr
. Wyznacz parametr 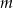 .
.
Dana jest funkcja 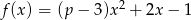 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 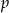 , dla których:
, dla których:
- największa wartość funkcji
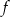 jest liczbą ujemną,
jest liczbą ujemną, - najmniejsza wartość funkcji
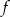 jest mniejsza od -2.
jest mniejsza od -2.
Naszkicuj wykres funkcji 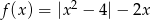 . Określ liczbę rozwiązań równania
. Określ liczbę rozwiązań równania 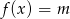 w zależności od wartości parametru
w zależności od wartości parametru 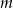 .
.
Dana jest funkcja kwadratowa 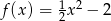 .
.
- Narysuj wykres funkcji
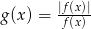 , której dziedziną jest zbiór
, której dziedziną jest zbiór 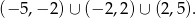
- Zapisz zbiór rozwiązań nierówności
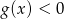 .
.
Naszkicuj wykres funkcji 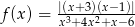 .
.
Naszkicuj wykres funkcji 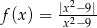 . Określ dziedzinę oraz zbiór wartości funkcji.
. Określ dziedzinę oraz zbiór wartości funkcji.
Dana jest funkcja 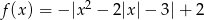 ;
; 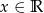 .
.
- Narysuj wykres tej funkcji, stosując odpowiednie przekształcenia, wymień je.
- Na podstawie wykresu funkcji
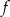 określ zbiór wartości tej funkcji.
określ zbiór wartości tej funkcji. - Podaj liczbę miejsc zerowych funkcji
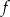 .
. - Podaj współrzędne punktu przecięcia wykresu z osią
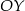 .
. - Podaj znak liczby
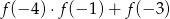 .
. - Czy funkcja jest rożnowartościowa? Czy jest parzysta lub nieparzysta?
Naszkicuj wykres funkcji 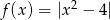 , a następnie określ liczbę rozwiązań równania
, a następnie określ liczbę rozwiązań równania 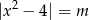 w zależności od wartości parametru
w zależności od wartości parametru 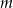 .
.
Dana jest funkcja 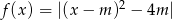 , gdzie
, gdzie 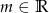 .
.
- Naszkicuj wykres funkcji
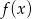 dla
dla 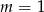 .
. - Dla jakich wartości parametru
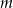 równanie
równanie 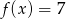 ma dokładnie trzy rozwiązania.
ma dokładnie trzy rozwiązania.
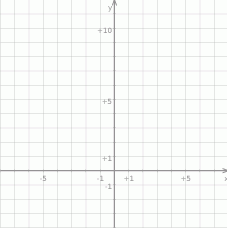
Narysuj wykres funkcji 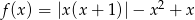 i odczytaj z niego ilość rozwiązań równania
i odczytaj z niego ilość rozwiązań równania 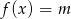 .
.
Narysuj wykres funkcji 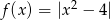 , a następnie wykres funkcji
, a następnie wykres funkcji 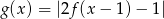 .
.

