Zestaw użytkownika nr 4022_8190
Funkcje-maturaCzas pracy: 60 min.
Określ dziedzinę funkcji 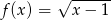 .
.
Wyznacz najmniejszą i największą wartość funkcji 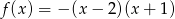 w przedziale
w przedziale 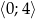 .
.
Oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego  jeżeli
jeżeli 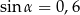 .
.
Określ dziedzinę funkcji 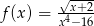 .
.
Funkcja 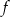 jest określona wzorem
jest określona wzorem 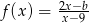 dla
dla 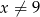 . Ponadto wiemy, że
. Ponadto wiemy, że 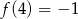 . Oblicz współczynnik
. Oblicz współczynnik 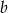 .
.
Wyznacz wszystkie wartości parametru 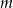 , dla których dziedziną funkcji
, dla których dziedziną funkcji
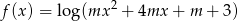
jest zbiór wszystkich liczb rzeczywistych.
Na rysunku przedstawiony jest wykres funkcji 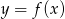 .
.
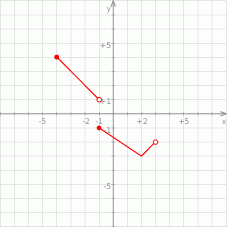
- Podaj zbiór wartości tej funkcji.
- Podaj dziedzinę tej funkcji.
- Wartość funkcji dla argumentu 2.
- Narysuj wykres funkcji
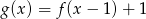 .
. - Narysuj wykres symetryczny do wykresu funkcji
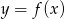 względem początku układu współrzędnych.
względem początku układu współrzędnych.
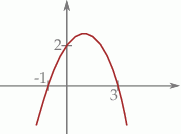
Na podstawie wykresu funkcji kwadratowej podaj jej wzór.
Na rysunku jest przedstawiony wykres funkcji 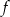 .
.
- Podaj dziedzinę funkcji
 .
. - Podaj wszystkie miejsca zerowe funkcji
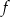 .
. - Odczytaj wartość funkcji
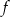 dla argumentu
dla argumentu 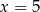 .
. - Podaj zbiór wartości funkcji
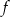 .
. - Podaj maksymalny przedział o długości 3, w którym funkcja
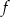 jest rosnąca.
jest rosnąca. - Zapisz w postaci sumy przedziałów zbiór wszystkich argumentów, dla których funkcja
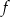 przyjmuje wartości ujemne.
przyjmuje wartości ujemne.
Określ dziedzinę funkcji 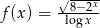 .
.
Sprawdź tożsamość: 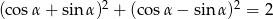 .
.
Wyznacz dziedzinę funkcji 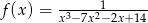 .
.
Wyznacz dziedzinę funkcji 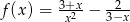 .
.
Określ dziedzinę funkcji 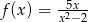 .
.
Określ dziedzinę funkcji 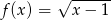 .
.
Wyznacz dziedzinę funkcji 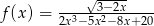 .
.
Wyznacz dziedzinę funkcji  .
.
Wyznacz dziedzinę funkcji 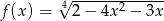 .
.

