Zestaw użytkownika nr 4103_9868
MATURA 2011Suma punktów: 50
Wyrażenie 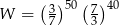 jest równe
jest równe
A) 1 B) 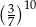 C)
C) 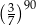 D)
D) 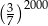
Rozwiązaniem równania 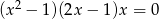 nie jest liczba
nie jest liczba
A) 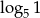 B)
B) 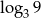 C)
C) 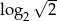 D)
D) 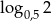
Odwrotność liczby będącej rozwiązaniem równania 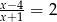 jest równa
jest równa
A) 6 B) 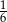 C)
C) 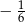 D)
D) 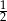
Liczba 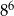 jest większa od liczby
jest większa od liczby 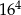
A) o 300% B) o 400% C) o 200% D) o 100%
Wyrażenie 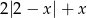 dla
dla 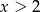 ma wartość
ma wartość
A) 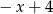 B)
B) 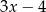 C) 1 D) 5
C) 1 D) 5
Wskaż liczbę, której 4% jest równe 8.
A) 3,2 B) 32 C) 100 D) 200
Liczbę 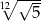 można zapisać inaczej w postaci
można zapisać inaczej w postaci
A) 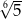 B)
B) 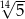 C)
C) 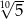 D)
D) 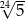
Zapisz wzór funkcji 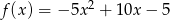 w postaci kanonicznej i iloczynowej.
w postaci kanonicznej i iloczynowej.
Dany jest trójmian kwadratowy 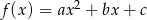 .
.
- Dla
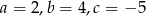 wyznacz największą i najmniejszą wartość tego trójmianu w przedziale
wyznacz największą i najmniejszą wartość tego trójmianu w przedziale 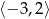 .
. - Wyznacz wzór trójmianu w postaci iloczynowej, jeśli wiadomo, że ma on miejsca zerowe
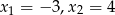 , a do jego wykresu należy punkt
, a do jego wykresu należy punkt 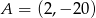 .
.
Wiedząc, że  jest kątem ostrym oraz
jest kątem ostrym oraz 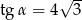 oblicz wartość wyrażenia
oblicz wartość wyrażenia 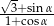 .
.
Mniejszą z dwóch liczb spełniających równanie 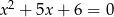 jest
jest
A) -6 B) -3 C) -2 D) -1
Ciągiem geometrycznym jest ciąg określony wzorem
A) 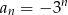 B)
B) 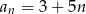 C)
C) 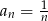 D)
D) 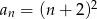
Liczba 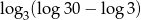 jest równa liczbie
jest równa liczbie
A) -1 B) 0 C) 1 D) 2
Objętość graniastosłupa prawidłowego trójkątnego jest równa 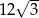 , a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
, a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 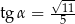 . Wówczas
. Wówczas
A) 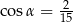 B)
B) 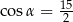 C)
C) 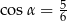 D)
D) 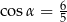
Oblicz wysokość prostopadłościanu, którego podstawa jest prostokątem o wymiarach 3 i 4, a pole powierzchni całkowitej wynosi 94.
Powierzchnia sześcianu wynosi 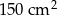 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 4 cm B) 5 cm C) 5,5 cm D) 6 cm
Oblicz 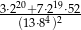 .
.
Liczba 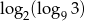 jest równa
jest równa
A) 1 B) -1 C) 2 D) -2
Przekątna graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości tego graniastosłupa. Z tego wynika, że miara kąta, jaki tworzy ta przekątna z podstawą, jest równa
A) 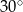 B)
B) 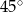 C)
C) 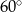 D)
D) 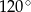
Jeśli 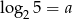 oraz
oraz 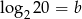 , to liczba
, to liczba 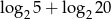 jest równa
jest równa
A) 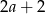 B)
B) 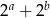 C)
C) 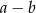 D)
D) 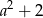
Pierwszy wyraz ciągu arytmetycznego jest równy -5, a suma dwudziestu początkowych wyrazów tego ciągu jest równa 1230. Wyznacz różnicę tego ciągu.
W ciągu arytmetycznym suma pierwszego i trzeciego wyrazu jest równa 2, a iloraz pierwszego i czwartego jest równy 1.
- Napisz wzór ogólny ciągu oraz wzór na sumę
 początkowych wyrazów tego ciągu.
początkowych wyrazów tego ciągu. - Wyznacz
 , dla których suma
, dla których suma  kolejnych, początkowych wyrazów ciągu jest mniejsza od 50.
kolejnych, początkowych wyrazów ciągu jest mniejsza od 50.
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 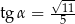 . Wówczas
. Wówczas
A) 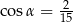 B)
B) 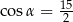 C)
C) 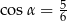 D)
D) 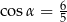
Wykaż tożsamość 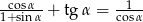 .
.

