Zestaw użytkownika nr 4114_7338

LOGARYTMY - MATURA

Zadanie 1

Wykaż, że liczba 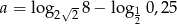√ - a = log2 28 − log12 0,25 jest liczbą wymierną.

Zadanie 2

Oblicz 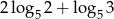2 log52 + log 53 .

Zadanie 3

Oblicz wartość wyrażenia 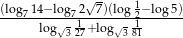(log 14−log 2√ 7)(log 1−log5) ---7-log√-71+-log√--21------ 327 3 81 .

Zadanie 4

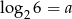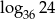Wiedząc, że log2 6 = a , wyznacz log 36 24 .

Zadanie 5

Oblicz 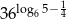log 5− 1 3 6 6 4 .

Zadanie 6

Nie używając kalkulatora, porównaj liczby: 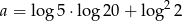2 a = log 5⋅log 20 + log 2 oraz ∘ -----√--- b = 6− 2 5 .

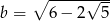Zadanie 7

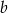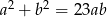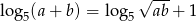Udowodnij, że jeśli liczby dodatnie i spełniają warunek 2 2 a + b = 23ab , to √ --- log5(a + b) = log 5 ab + 1 .

Zadanie 8

Ciąg geometryczny 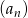(an) jest określony wzorem 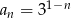1−n an = 3 dla n ≥ 1 .

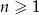Oblicz iloraz tego ciągu.
Oblicz 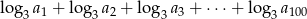czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.

Zadanie 9

Wykaż, że 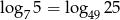lo g75 = log 4925 .

Zadanie 10

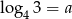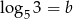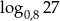Widząc, że log4 3 = a i log 53 = b , wyznacz log 0,827 w zależności od i .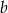

Zadanie 11

Oblicz 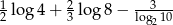1 2 --3--- 2 log 4+ 3 log 8− log210 .

Zadanie 12

Wiadomo, że 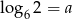log 62 = a . Wyznacz 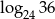log2436 w zależności od .

Zadanie 13

Oblicz wartość wyrażenia 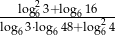log2 3+ log 16 log-36⋅log-486+log2-4 6 6 6 .

Zadanie 14

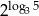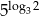Udowodnij, że liczby log 5 2 3 i log 2 5 3 są równe.

Arkusz Wersja PDF