Zestaw użytkownika nr 4117_1087
Zestaw użytkownika
nr 4117_1087
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 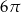 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 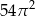 B)
B) 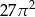 C)
C) 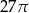 D)
D) 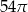
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 2, a krawędź boczna długość 6.
Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma miarę 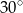 . Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
. Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
Podstawą graniastosłupa prawidłowego jest trójkąt, w którym długość wysokości wynosi 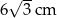 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt o mierze
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt o mierze 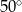 . Oblicz pole powierzchni całkowitej i objętość graniastosłupa. Wynik podaj z dokładnością do 1cm.
. Oblicz pole powierzchni całkowitej i objętość graniastosłupa. Wynik podaj z dokładnością do 1cm.
Dany jest ostrosłup prawidłowy czworokątny 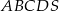 o podstawie
o podstawie 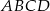 . Pole trójkąta
. Pole trójkąta 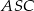 jest równe 120, a cosinus kąta
jest równe 120, a cosinus kąta 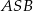 jest równy
jest równy 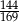 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Podstawą ostrosłupa 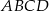 jest trójkąt
jest trójkąt 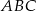 . Krawędź
. Krawędź 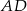 jest wysokością ostrosłupa (zobacz rysunek).
jest wysokością ostrosłupa (zobacz rysunek).
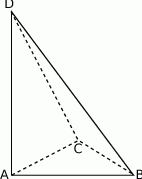
Oblicz objętość ostrosłupa  , jeśli wiadomo, że
, jeśli wiadomo, że  .
.
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 18 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 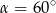 . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt
. Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt  .
.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 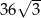 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
, a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 6, a pole ściany bocznej jest równe 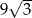 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa jest prostokąt o bokach 6cm i 8cm. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod katem 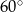 . Oblicz pole powierzchni ostrosłupa.
. Oblicz pole powierzchni ostrosłupa.
Podstawą ostrosłupa 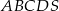 jest kwadrat
jest kwadrat  (patrz rysunek).
(patrz rysunek).
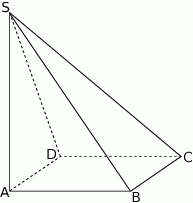
Krawędź  jest wysokością tego ostrosłupa. Odległość punktu
jest wysokością tego ostrosłupa. Odległość punktu  od krawędzi
od krawędzi 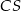 jest równa
jest równa 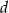 , a kąt dwuścienny między ścianami
, a kąt dwuścienny między ścianami 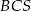 i
i 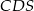 ma miarę
ma miarę 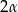 , gdzie
, gdzie 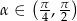 . Oblicz:
. Oblicz:
- odległość punktu
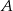 od krawędzi
od krawędzi 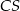
- wysokość tego ostrosłupa.

