Zestaw użytkownika nr 4119_6187
Zestaw użytkownika
nr 4119_6187
Na rysunku przedstawiono liczbę i rodzaj kul umieszczonych w każdym z czterech pudełek. Z każdego pudełka losujemy jedną kulę.
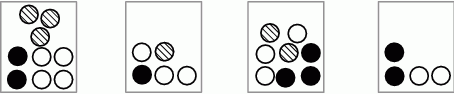
Prawdopodobieństwo wylosowania białej kuli jest największe, gdy kulę losujemy z pudełka
A) 2 B) 1 C) 3 D) 4
Średni wiek w pewnej sześcioosobowej grupie tematycznej na konferencji naukowej wynosił 49 lat. Najmłodszy uczestnik zrezygnował i wówczas średnia wieku wzrosła do 53 lat. Ile lat miał najmłodszy uczestnik?
W woreczku są tylko koraliki białe i czerwone. Białych koralików jest cztery razy więcej niż czerwonych. Losujemy jeden koralik. Prawdopodobieństwo, że wylosujemy biały koralik, jest równe
A) 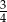 B)
B) 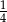 C)
C)  D)
D) 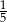
Średnia arytmetyczna liczb: 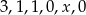 jest równa 2. Oblicz
jest równa 2. Oblicz  .
.
Kod dostępu do komputera Andrzeja złożony jest z czterech kolejnych wielokrotności liczby 7 ustawionych od najmniejszej do największej. Suma tych wielokrotności wynosi 294. Znajdź liczby, z których złożony jest ten kod. Zapisz swoje rozumowanie.
Do pięciu różnych naczyń rozlano 6 litrów wody.
Średnia arytmetyczna ilości wody w tych naczyniach zmieni się, gdy
A) jedno naczynie opróżnimy, przelewając jego zawartość do pozostałych naczyń.
B) do każdego naczynia dolejemy taką samą ilość wody.
C) z czterech naczyń odlejemy trochę wody do piątego naczynia.
D) poprzelewamy wodę z jednego naczynia do drugiego, tak by w każdym naczyniu było jej tyle samo.
Do zestawu liczb: 1, 6, 8, 13, 13 dopisano jeszcze jedną liczbę. Mediana powiększonego zestawu wynosi 7.
Którą z poniższych liczb dopisano?
A) 9 B) 8 C) 6 D) 7
Średnia arytmetyczna liczb 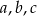 jest równa 15. Oblicz średnią arytmetyczną liczb
jest równa 15. Oblicz średnią arytmetyczną liczb 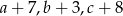 .
.
Na przyjęciu spotkała się pewna liczba znajomych. Wszyscy znajomi przywitali się podaniem ręki. Nastąpiło 10 powitań. Ilu przyjaciół się spotkało?
W turnieju karate rozegrano 36 walk. Każdy walczył z każdym dokładnie raz. Ilu zawodników brało udział w turnieju?
Ile jest liczb pięciocyfrowych, spełniających jednocześnie następujące cztery warunki:
(1) cyfry setek, dziesiątek i jedności są parzyste,
(2) cyfra setek jest większa od cyfry dziesiątek,
(3) cyfra dziesiątek jest większa od cyfry jedności,
(4) w zapisie tej liczby nie występuje cyfra 9.
Rzucamy trzy razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 12.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że w każdym rzucie otrzymamy inną liczbę oczek.
Rzucamy sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że wypadną co najmniej dwa oczka.
Spośród 5 monet jednozłotowych, 7 dwuzłotowych i 6 pięciozłotowych wybieramy 3 monety. Oblicz prawdopodobieństwo, że wszystkie trzy monety będą miały ten sam nominał.
Co jest bardziej prawdopodobne: wyrzucić dwa orły w trzech rzutach monetą, czy trzy orły w czterech rzutach?

