Zestaw użytkownika nr 4128_2749
Zestaw użytkownika
nr 4128_2749
Zadanie 1
(1 pkt)
Okrąg o równaniu 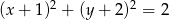 :
:
A) nie przecina osi 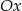 ,
,
B) nie przecina osi 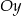 ,
,
C) przechodzi przez początek układu współrzędnych,
D) przechodzi przez punkt 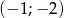 .
.
Zadanie 2
(1 pkt)
Proste 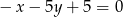 i
i 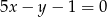 przecinają się pod kątem o mierze
przecinają się pod kątem o mierze
A) 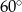 B)
B) 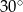 C)
C) 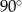 D)
D) 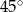
Zadanie 3
(1 pkt)
Prosta 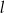 ma równanie
ma równanie 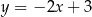 . Równaniem prostej prostopadłej do
. Równaniem prostej prostopadłej do 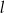 i przechodzącej przez punkt
i przechodzącej przez punkt 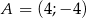 jest:
jest:
A) 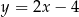 B)
B) 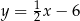 C)
C) 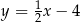 D)
D) 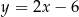
Zadanie 4
(1 pkt)
Środek 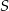 okręgu o równaniu
okręgu o równaniu 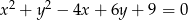 ma współrzędne
ma współrzędne
A) 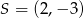 B)
B) 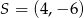 C)
C) 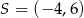 D)
D) 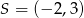
Zadanie 5
(1 pkt)
Punkty 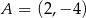 i
i 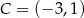 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 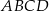 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 100 B) 50 C) 25 D) 12,5
Zadanie 6
(3 pkt)
Wykaż, że prosta 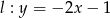 jest styczna do okręgu
jest styczna do okręgu 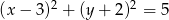 .
.
Zadanie 7
(2 pkt)
W układzie współrzędnych na płaszczyźnie punkty 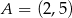 i
i 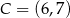 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 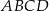 . Wyznacz równanie prostej
. Wyznacz równanie prostej 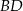 .
.
Zadanie 8
(2 pkt)
Określ wzajemne położenie prostych 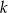 i
i 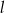 o równaniach
o równaniach