Zestaw użytkownika nr 4172_8303
Zestaw użytkownika
nr 4172_8303
Ciąg 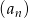 , gdzie
, gdzie 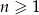 , jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji
, jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji 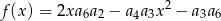 .
.
Dany jest ciąg o wyrazie ogólnym 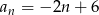 . Wybierz sto kolejnych początkowych wyrazów ciągu
. Wybierz sto kolejnych początkowych wyrazów ciągu 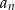 i oblicz dla jakiej liczby naturalnej
i oblicz dla jakiej liczby naturalnej 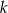 stosunek wyrazu stojącego na miejscu
stosunek wyrazu stojącego na miejscu 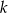 , licząc od początku, do wyrazu stojącego na miejscu
, licząc od początku, do wyrazu stojącego na miejscu 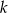 , licząc od końca, jest równy
, licząc od końca, jest równy 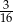 .
.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego wynosi 6, a suma 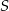 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 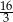 . Dla jakich naturalnych
. Dla jakich naturalnych  spełniona jest nierówność
spełniona jest nierówność 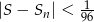 ?
?
Długości boków trójkąta są kolejnymi wyrazami rosnącego ciągu geometrycznego o ilorazie 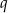 , a cosinus jednego z jego kątów jest równy
, a cosinus jednego z jego kątów jest równy 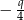 .
.
- Wyznacz
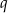 .
. - Wiedząc, że promień okręgu opisanego na tym trójkącie ma długość
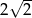 , oblicz pole tego trójkąta.
, oblicz pole tego trójkąta.
Ciąg 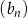 jest nieskończonym ciągiem liczb dodatnich, a ciąg
jest nieskończonym ciągiem liczb dodatnich, a ciąg 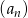 spełnia warunek
spełnia warunek
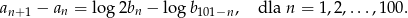
Oblicz 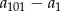 .
.
Pierwszy, trzeci i jedenasty wyraz ciągu arytmetycznego o różnicy 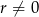 są kolejnymi wyrazami ciągu geometrycznego o ilorazie
są kolejnymi wyrazami ciągu geometrycznego o ilorazie 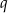 . Dla jakich wartości parametru
. Dla jakich wartości parametru 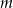 funkcja
funkcja 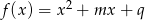 osiąga minimum większe od -196?
osiąga minimum większe od -196?
Wykaż, że jeżeli liczby 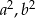 i
i 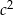 tworzą ciąg arytmetyczny, który nie jest stały, to liczby
tworzą ciąg arytmetyczny, który nie jest stały, to liczby 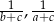 i
i 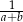 również tworzą ciąg arytmetyczny.
również tworzą ciąg arytmetyczny.
W ciągu arytmetycznym o nieparzystej liczbie wyrazów suma wyrazów stojących na miejscach nieparzystych równa się 44, a suma pozostałych wynosi 33. Znajdź wyraz środkowy i liczbę wyrazów tego ciągu.
Ciąg 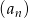 dany jest wzorem
dany jest wzorem 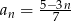 , dla
, dla 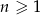 .
.
- Oblicz sumę
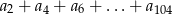 .
. - Ustalmy
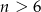 . Dla jakich
. Dla jakich  liczby
liczby 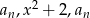 są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 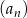 dla każdego
dla każdego 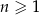 określona jest wzorem
określona jest wzorem 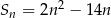 .
.
- Wykaż, że ciąg
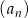 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym. - Wykaż, że jeżeli suma
 początkowych wyrazów ciągu dla każdego
początkowych wyrazów ciągu dla każdego 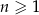 określona jest wzorem
określona jest wzorem 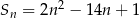 , to ciąg ten nie jest arytmetyczny.
, to ciąg ten nie jest arytmetyczny. - Znajdź takie trzy kolejne wyrazy ciągu
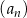 , aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.
, aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.

