Zestaw użytkownika nr 4190_5162
Zestaw użytkownika
nr 4190_5162
Rozwiąż nierówność 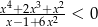 .
.
Suma drugiego, czwartego i szóstego wyrazu ciągu arytmetycznego jest równa 42, zaś suma kwadratów wyrazów drugiego i trzeciego jest równa 185. Wyznacz pierwszy wyraz i różnicę tego ciągu.
Określ liczbę pierwiastków równania 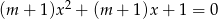 w zależności od wartości parametru
w zależności od wartości parametru 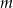 , a następnie naszkicuj wykres funkcji:
, a następnie naszkicuj wykres funkcji:

Dziedziną funkcji 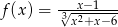 jest zbiór
jest zbiór
A) 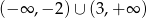 B)
B) 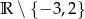 C)
C) 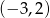 D)
D) 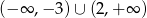
Dany jest wielomian 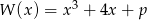 , gdzie
, gdzie 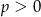 jest liczbą pierwszą. Znajdź
jest liczbą pierwszą. Znajdź 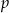 wiedząc, że
wiedząc, że 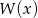 ma pierwiastek całkowity.
ma pierwiastek całkowity.
Wyrażenie 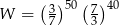 jest równe
jest równe
A) 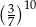 B)
B) 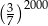 C) 1 D)
C) 1 D) 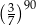
Znajdź wszystkie liczby całkowite spełniające nierówność 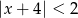 .
.
Znajdź liczby  i
i 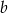 wiedząc, że suma liczby
wiedząc, że suma liczby  i potrojonej liczby
i potrojonej liczby 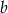 jest równa 36, a iloczyn liczb a i b jest największy z możliwych.
jest równa 36, a iloczyn liczb a i b jest największy z możliwych.
Pierwiastkami trójmianu kwadratowego 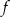 o współczynniku -3 przy najwyższej potędze są liczby
o współczynniku -3 przy najwyższej potędze są liczby 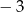 . Oblicz
. Oblicz 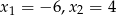 .
.
W sześciokącie foremnym połączono środki sąsiednich boków otrzymując ponownie sześciokąt foremny. Oblicz stosunek pól: otrzymanego i wyjściowego sześciokąta.
Rozwiąż nierówność 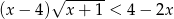 .
.
Skróć ułamek 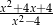 .
.

