Zestaw użytkownika nr 4295_7167
Zestaw użytkownika
nr 4295_7167
Wykonując rozmowę telefoniczną płacimy 63 grosze za połączenie oraz 42 grosze za każdą minutę połączenia. Ile minut trwała rozmowa, której łączny koszt wyniósł 16,17 zł?
A) 38 B) 43 C) 36 D) 37
Uczniowie klasy IIa uczący się języka niemieckiego stanowią 15% wszystkich uczniów klas drugich swojej szkoły. Ponadto 62,5% uczniów klasy IIa uczy się niemieckiego. Wśród wszystkich uczniów klas drugich swojej szkoły, uczniowie klasy IIa stanowią
A) 38,5% B) 0,24% C) 2,4% D) 24%
Funkcją malejącą jest funkcja
A) 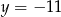 B)
B) 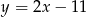 C)
C) 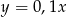 D)
D) 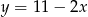
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 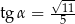 . Wówczas
. Wówczas
A) 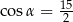 B)
B) 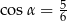 C)
C) 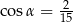 D)
D) 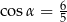
Kąt  jest ostry i
jest ostry i 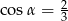 . Wartość wyrażenia
. Wartość wyrażenia 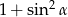 jest równa
jest równa
A) 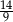 B)
B) 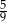 C)
C)  D)
D) 
Liczba 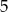 nie należy do dziedziny wyrażenia
nie należy do dziedziny wyrażenia
A) 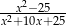 B)
B) 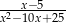 C)
C) 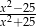 D)
D) 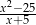
Zbiór 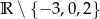 jest dziedziną wyrażenia:
jest dziedziną wyrażenia:
A) 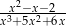 B)
B) 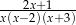 C)
C) 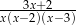 D)
D) 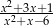
Ze zbioru 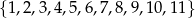 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 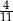 B)
B) 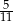 C)
C) 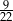 D)
D) 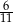
Zbiorem wartości funkcji kwadratowej 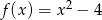 jest
jest
A) 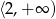 B)
B) 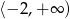 C)
C) 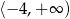 D)
D) 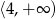
Największą wartością funkcji kwadratowej 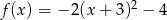 jest
jest
A) 3 B) -4 C) 4 D) -2
Pierwiastkami wielomianu stopnia trzeciego 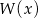 są liczby
są liczby 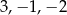 , a współczynnik stojący przy najwyższej potędze zmiennej
, a współczynnik stojący przy najwyższej potędze zmiennej  jest równy 3. Wielomian ten można zapisać w postaci
jest równy 3. Wielomian ten można zapisać w postaci
A) 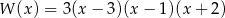
B) 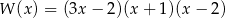
C) 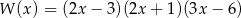
D) 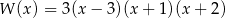
Rozwiąż nierówność 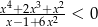 .
.
Oblicz wyrazy 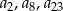 ciągu arytmetycznego jeśli
ciągu arytmetycznego jeśli 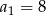 i
i 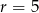 .
.
Wyniki klasówki z matematyki, której średnia ocen była równa 3,5 przedstawiono w tabeli.
| Oceny | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba uczniów | 2 | 2 |  | 9 | 3 | 2 |
- Oblicz
 .
. - Oblicz medianę danych.
Rozwiąż nierówność: 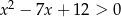 .
.
Cenę płaszcza zimowego obniżono wiosną o 15% i wówczas cena wynosiła 510 zł. Oblicz cenę płaszcza przed obniżką.
Na wycieczkę wyjechało 38 uczniów. Dzieci spały w 15 pokojach. Dziewczynki spały w pokojach dwuosobowych, a chłopcy spali w pokojach trzyosobowych. Wszystkie miejsca w pokojach były zajęte. Ile dziewczynek i ilu chłopców było na wycieczce? Zapisz obliczenia.
Za wynajęcie autobusu na wycieczkę uczniowie klasy IA mieli zapłacić 1800 złotych. Ponieważ 4 uczniów zrezygnowało z tej wycieczki, każdy z pozostałych uczniów zapłacił o 15 zł więcej. Oblicz, ilu uczniów jest w klasie IA.
Średni wiek w pewnej sześcioosobowej grupie tematycznej na konferencji naukowej wynosił 49 lat. Najmłodszy uczestnik zrezygnował i wówczas średnia wieku wzrosła do 53 lat. Ile lat miał najmłodszy uczestnik?
Samochód przebył w pewnym czasie 210 km. Gdyby jechał ze średnią prędkością o 10 km/h większą, to czas przejazdu skróciłby się o pół godziny. Oblicz, z jaką średnią prędkością jechał ten samochód.
Wyznacz odległość punktu 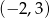 od prostej o równaniu
od prostej o równaniu 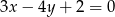 .
.
W układzie współrzędnych na płaszczyźnie punkty 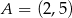 i
i 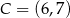 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 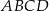 . Wyznacz równanie prostej
. Wyznacz równanie prostej 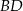 .
.
Obwód czworokąta wypukłego 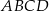 jest równy 50 cm. Obwód trójkąta
jest równy 50 cm. Obwód trójkąta 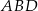 jest równy 46 cm, a obwód trójkąta
jest równy 46 cm, a obwód trójkąta 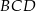 jest równy 36 cm. Oblicz długość przekątnej
jest równy 36 cm. Oblicz długość przekątnej 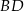 .
.
Boki prostokąta 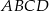 mają długości 5 i 12. Oblicz odległość wierzchołka
mają długości 5 i 12. Oblicz odległość wierzchołka 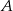 od przekątnej
od przekątnej 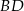 .
.
Podstawą ostrosłupa 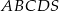 jest prostokąt
jest prostokąt 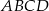 o bokach długości
o bokach długości 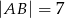 i
i 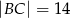 . Krawędź
. Krawędź 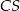 jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt
jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 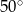 . Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.

