Zestaw użytkownika nr 4314_1688
Zestaw użytkownika
nr 4314_1688
Dana jest funkcja 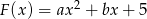 . Wyznacz
. Wyznacz  i
i 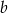 wiedząc, że
wiedząc, że 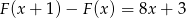 .
.
Wyznacz wszystkie wartości parametru 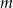 , dla których funkcja
, dla których funkcja 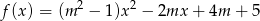 jest rosnąca w przedziale
jest rosnąca w przedziale 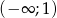 i malejąca w przedziale
i malejąca w przedziale 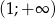 .
.
Naszkicuj wykres funkcji, która każdej liczbie rzeczywistej 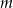 przyporządkowuje liczbę pierwiastków równania
przyporządkowuje liczbę pierwiastków równania
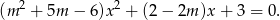
Wyznacz te wartości parametru  , dla których różne pierwiastki
, dla których różne pierwiastki 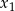 i
i 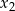 równania
równania 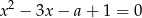 spełniają warunek
spełniają warunek 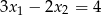 .
.
Dla jakich wartości parametru 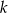 miejsca zerowe funkcji
miejsca zerowe funkcji 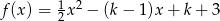 należą do przedziału
należą do przedziału 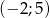 ?
?
Wykaż, że dla dowolnych liczb rzeczywistych  ,
, 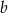 i
i  , funkcja
, funkcja
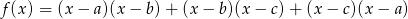
ma co najmniej jedno miejsce zerowe.
Wyznacz wszystkie wartości 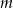 , dla których nierówność
, dla których nierówność 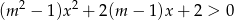 jest prawdziwa dla każdego
jest prawdziwa dla każdego 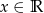 .
.
Rozwiąż nierówność 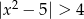 .
.
Rozwiąż nierówność 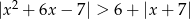 .
.
Wyznacz liczbę rozwiązań równania 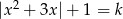 w zależności od parametru
w zależności od parametru 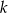 .
.
Rozwiąż równanie 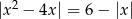 .
.
Rozwiąż równanie 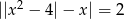 .
.
Zbadaj liczbę rozwiązań równania 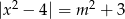 w zależności od parametru
w zależności od parametru 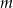 .
.
Rozwiąż graficznie i algebraicznie układ równań
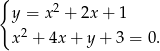
Rozwiąż układ równań 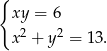
Samochód przebył w pewnym czasie 210 km. Gdyby jechał ze średnią prędkością o 10 km/h większą, to czas przejazdu skróciłby się o pół godziny. Oblicz, z jaką średnią prędkością jechał ten samochód.
Dwa pociągi towarowe wyjechały z miast 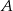 i
i 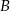 oddalonych od siebie o 540 km. Pociąg jadący z miasta
oddalonych od siebie o 540 km. Pociąg jadący z miasta 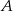 do miasta
do miasta 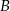 wyjechał o godzinę wcześniej niż pociąg jadący z miasta
wyjechał o godzinę wcześniej niż pociąg jadący z miasta 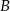 do miasta
do miasta 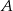 i jechał z prędkością o 9 km/h mniejszą. Pociągi te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te pociągi.
i jechał z prędkością o 9 km/h mniejszą. Pociągi te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te pociągi.
Z murów zamku wystrzelono pocisk armatni, który po 4 sekundach spadł na ziemię. Wysokość (w metrach), na jaką wzniósł się pocisk (względem poziomu armaty) po upływie 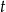 sekund od momentu wystrzelenia opisuje funkcja
sekund od momentu wystrzelenia opisuje funkcja 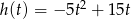 , gdzie
, gdzie 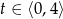 .
.
- Oblicz po jakim czasie pocisk ponownie znalazł się na wysokości z jakiej został wystrzelony.
- Oblicz na jaką maksymalną wysokość względem ziemi wzniósł się ten pocisk.
Łódź musi płynąć 60km w dół rzeki, a następnie 10km w górę rzeki. Prędkość prądu rzeki wynosi 5km/godz. Jaka powinna być prędkość własna łodzi, aby cała podróż nie trwała dłużej niż 10 godzin?
Szkoła zamówiła seans filmowy dla uczniów klas trzecich. Koszt seansu wyniósł 1650 zł. Ponieważ do kina nie przyszło 15 uczniów, pozostali musieli dopłacić po 1 zł za bilet. Jaka była planowana, a jaka rzeczywista cena biletów?
Właściciel sklepu z odzieżą kupił w hurtowni koszulki, płacąc za nie 720 zł. Gdyby każda koszulka kosztowała o 2 złote mniej, to za tę samą kwotę mógłby kupić o 5 koszulek więcej. Oblicz, ile koszulek kupił w tej hurtowni wspomniany właściciel sklepu. Podaj cenę jednej koszulki.
W dwóch hotelach wybudowano prostokątne baseny. Basen w pierwszym hotelu ma powierzchnię 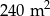 . Basen w drugim hotelu ma powierzchnię
. Basen w drugim hotelu ma powierzchnię 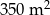 oraz jest o 5 m dłuższy i 2 m szerszy niż w pierwszym hotelu. Oblicz, jakie wymiary mogą mieć baseny w obu hotelach. Podaj wszystkie możliwe odpowiedzi.
oraz jest o 5 m dłuższy i 2 m szerszy niż w pierwszym hotelu. Oblicz, jakie wymiary mogą mieć baseny w obu hotelach. Podaj wszystkie możliwe odpowiedzi.
Pole każdej z dwóch prostokątnych działek jest równe 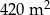 . Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 14 m mniejsza. Oblicz szerokość i długość każdej z działek.
. Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 14 m mniejsza. Oblicz szerokość i długość każdej z działek.
Na szczyt góry wożą narciarzy 3 wyciągi: gondolowy, krzesełkowy i orczykowy. Gondolowy wwozi grupę 1200 narciarzy o 2 godziny krócej niż krzesełkowy i 3 razy szybciej niż orczykowy. Jeżeli wszystkie wyciągi są czynne to grupa 1200 narciarzy wjeżdża na szczyt w ciągu 2 godzin. Ilu narciarzy wjeżdża na szczyt w ciągu 1 godziny każdym wyciągiem?

